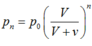Một cái bình có thể tích V nối với bơm hút có thể tích xilanh v . áp suất khí quyển là p o . sau n lần bơm thì áp suất trong bình giảm từ p o đến giá trị p n . Tính p n (bơm chậm để nhiệt độ không đổi).
A. 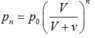
B. 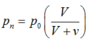
C. 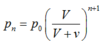
D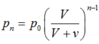
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Xét khối khí trong bóng sau 12 lần bơm. Trước khi bơm vào bóng, khối khí đó có thể tích là: V0=12.0,125+2,5=4 l và áp suất của khối khí đó ban đầu là P0 = 1atm. Sau khi bơm vào bóng thể tích của khối khí đó là V = 2,5l và áp suất của quá trình đó là P
Vì nhiệt độ là không đổi trong suốt quá trình bơm, do đó áp dụng định luật Bôi-lơ-ma-ri-ốt, ta có:
![]()
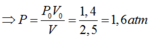

Gọi V0 là thể tích mỗi lần bơm
V 0 = S . h = 10.30 = 300 ( c m 3 ) = 0 , 3 ( l )
Mà p = 4p0
Ta có: ( n V 0 ) . p 0 = p . V ⇒ n = p . V p 0 . V 0 = 4.3 0 , 3 = 40 l ầ n

Chọn C.
Áp suất trong bánh xe khi bơm xong: p = p0 + p’
Với p’ = F/S = 350/0,005 = 0,7.105 Pa;
→ p = 1,7.105 Pa lớn hơn 1,5p0 nên thể tích sau khi bơm là 2000 cm3.
Mỗi lần bơm có 8.25 = 200 cm3 không khí ở áp suất p0 được đưa vào bánh xe. Sau n lần bơm có 200n cm3 không khí được đưa vào bánh. Ban đầu có 1500 cm3 không khí ở áp suất p0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p1 = p0; V1 = (1500 + 200n)
Trạng thái 2: p2 = 1,7.105 Pa; V2 = 2000 cm3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần

Chọn C.
Áp suất trong bánh xe khi bơm xong: p = p 0 + p’
Với p’ = F/S = 350/0,005 = 0,7. 10 5 Pa;
→ p = 1,7. 10 5 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3 .
Mỗi lần bơm có 8.25 = 200 c m 3 không khí ở áp suất p 0 được đưa vào bánh xe. Sau n lần bơm có 200n c m 3 không khí được đưa vào bánh. Ban đầu có 1500 c m 3 không khí ở áp suất p 0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p 1 = p 0 ; V1 = (1500 + 200n)
Trạng thái 2: p 2 = 1,7. 10 5 Pa; V2 = 2000 c m 3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần

Áp suất trong bánh xe khi bơm xong: p = p0 + p’
Với p’ = 350/0,005= 0,7. 10 5 Pa; p = 1,7.105 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3
Mỗi lần bơm có 8.25 = 200 c m 3 không khí ở áp suất p 0 được đưa vào bánh xe. Sau n lần bơm có 200n c m 3 không khí được đưa vào bánh. Ban đầu có 1500 c m 3 không khí ở áp suất p 0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p 1 = p 0 ; V 1 = (1500 + 200n)
Trạng thái 2: p 2 = 1,7. 10 5 Pa ; V 2 = 2000 c m 3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần.
Đáp án A
Sau lần bơm thứ nhất, áp suất là
Sau n lần bơm thì áp suất là: