Một nhóm bạn có 4 bạn gồm 2 bạn Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan
a) Tính số phần tử của không gian mẫu
A. 6
B. 24
C. 1
D. 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 4 2019
c. Trường hợp 1: bạn nam ngồi đầu. khi dó 2 bạn nam xếp vào 2 chỗ ( số ghế 1 và 3), nữ xếp nốt vào hai chỗ còn lại ( ghế số 2 và 4), số cách xếp là 2!.2!=4
Trường hợp 2: bnạ nữ ngồi đầu. Tương tự có 4 cách xếp . Vậy theo quy tắc cộng số phần tử của biến cố N là 4+4=8
Chọn C
CM
1 tháng 2 2018
b. đánh số ghế theo thứ tự 1,2,3,4. Hai bạn nam ngồi cạnh nhau ở vị trí ( 1 và 2) hoặc (2 và 3) hoặc (3 và 4). Nếu hai bạn nam đổi chỗ cho nhau( giữ nguyên chỗ hai bạn nữ) thì Ta có một cách xếp mới . vì vậy cần chọn phương án D
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
+) Xếp 4 bạn vào 4 ghế là sự hoán vị của 4 phần tử. Do đó, không gian mẫu là: \(n\left( \Omega \right) = 4!\) ( phần tử)
a) +) Gọi A là biến cố “Bạn Thảo ngồi ghế đầu tiên”
Ghế đầu tiên là ghế của Thảo nên có 1 cách chọn, 3 ghế còn lại xếp tùy ý 3 bạn nên ta có sự hoán vị của 3 phần tử. Theo quy tắc nhân, ta có: \(n\left( A \right) = 1.3!\) ( phần tử)
+) Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{4}\)
b) +) Gọi B là biến cố “Bạn Thảo ngồi ghế đầu tiên và bạn Huy ngồi ghế cuối cùng”.
Ghế đầu tiên của bạn Thảo và ghế cuối cùng của bạn Huy nên có 1 cách chọn cho cả 2 ghế, 2 ghế còn lại xếp tùy ý 2 bạn nên ta có sự hoán vị của 2 phần tử. Theo quy tắc nhân, ta có: \(n\left( B \right) = 1.1.2!\) ( phần tử)
+) Vậy xác suất của biến cố B là: \(P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{1}{{12}}\)
CM
9 tháng 1 2017
Chọn A
Ta đánh số các vị trí từ 1 đến 8.
Số phần tử không gian mẫu là 
Gọi A là biến cố: “xếp được tám bạn thành hàng dọc thỏa mãn các điều kiện: đầu hàng và cuối hàng đều là nam và giữa hai bạn nam gần nhau có ít nhất một bạn nữ, đồng thời bạn Quân và bạn Lan không đứng cạnh nhau”.
TH1: Quân đứng vị trí 1 hoặc 8 => có 2 cách
Chọn một trong 3 bạn nam xếp vào vị trí 8 hoặc 1 còn lại => có 3 cách.
Xếp 2 bạn nam còn lại vào 2 trong 4 vị trí 3,4,5,6 mà 2 nam không đứng cạnh nhau
=> có 6 cách
Xếp vị trí bạn Lan có 3 cách.
Xếp 3 bạn nữ vào 3 vị trí còn lại có 3! cách.
=> TH này có: 2.3.6.3.3! = 648 cách
TH2: Chọn 2 bạn nam ( khác Quân) đứng vào 2 vị trí 1 hoặc 8 có A 3 2 cách.
Xếp Quân và bạn nam còn lại vào 2 trong 4 vị trí 3,4,5,6 mà 2 nam không đứng cạnh nhau => có 6 cách
Xếp vị trí bạn Lan có 2 cách.
Xếp 3 bạn nữ vào 3 vị trí còn lại có 3! cách.
=> TH này có: 
Vậy xác suất của biến cố A là 
1 tháng 4 2019
Trả lời:
Thứ tự đúng là:
1) An 2) Bắc 3) Dũng 4) Huệ 5) Lan
CM
15 tháng 1 2019
Chọn A
Số phần tử của không gian mẫu: n ( Ω ) = 5!
Gọi A:”Hai bạn An và Bình không ngồi cạnh nhau”
Thì A ¯ :”Hai bạn An và Bình ngồi cạnh nhau”
Xếp An và Bình ngồi cạnh nhau coi như 1 phần tử
- Xếp 1 phần tử (An+Bình) và 3 bạn còn lại theo các thứ tự khác nhau có: 4! Cách
- Xếp 2 học sinh An và Bình ngồi cạnh nhau có 2! cách
Suy ra 
CM
2 tháng 1 2020
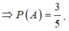
Đáp án là A
Vì có 5 bạn học sinh
⇒ nên số cách cho bạn Chi ngồi chính giữa là:
1 cách.
Bốn bạn còn lại xếp vào bốn ghế
⇒ chính là hoán vị của 4 phần tử nên có 4! cách.
Vậy có 1 . 4 ! = 24 cách
a. Mỗi cách xắp sêp 4 bạn vào 4 chỗ ngồi là một hoán vị của 4 phần tử. Vì vậy số phần tử của không gian mẫu là 4! =24
Chọn B