Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Số cách sắp xếp 20 bạn để ngồi vào hàng đầu tiên là: \(A_{60}^{20}\) (cách)
b, Sau khi sắp xếp xong hàng đầu tiên, số cách sắp xếp 20 bạn để ngồi vào hàng thứ hai là: \(A_{40}^{20}\) (cách)
c, Sau khi sắp xếp xong hai hàng đầu, số cách sắp xếp 20 bạn để ngồi vào hàng thứ ba là: \({P_{20}} = 20!\) (cách)

Mỗi cách sắp xếp 6 bạn vào 6 chiếc ghế trống là hoán vị của 6 chiếc ghế. Do đó, số cách sắp xếp chỗ ngồi cho các thành viên trong nhóm là
\({P_6} = 6! = 720\) (cách)

Lời giải:
Giả sử ban đầu có $a$ dãy ghế thì mỗi dãy có $b$ người. Trong đó $a,b$ là số tự nhiên $\neq 0$. Ta có: $ab=150(1)$
Khi thêm 71 người thì có tổng $150+71=221$ người.
Số dãy ghế: $a+2$
Số người mỗi dãy: $b+3$
Ta có: $(a+2)(b+3)=221(2)$
Từ $(1); (2)\Rightarrow 3a+2b=65$
$\Rightarrow b=\frac{65-3a}{2}$. Thay vào $(1)$ thì:
$a.\frac{65-3a}{2}=150$
$\Leftrightarrow a(65-3a)=300$
$\Leftrightarrow 3a^2-65a+300=0$
$\Leftrightarrow a=15$ (chọn) hoặc $a=\frac{20}{3}$ (loại)
Vậy có $15$ dãy ghế.

a) Mỗi cách sắp xếp 5 bạn học sinh vào 5 chiếc ghế là một hoán vị của 5 bạn học sinh. Do đó, số cách sắp xếp 5 bạn học sinh ngồi vào 5 cái ghế là hoán vị là:
\({P_5} = 5!\) (cách)
b) Khi bạn Nga nhất định ngồi vào chiếc ghế ngoài cùng bên trái, thì số cách sắp xếp là số cách sắp xếp 4 bạn còn lại vào 4 chiếc ghế, mỗi cách như vậy là một hoán vị của 4 bạn học sinh. Do đó, số cách sắp xếp là:
\({P_4} = 4! = 24\) (cách)

Số cách xếp bạn nữ: 10!
Số cách xếp bạn nam: 10!
Xếp cả nam và nữ có 2 trường hợp
=> 10! x 10! x 2

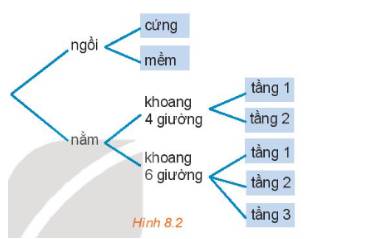
a) Số vé ghế ngồi là 2 (loại vé)
Số vé giường nằm là 2 + 3 = 5 (loại vé)
b) Số loại vé để bạn An lựa chọn là:
2 + 5 = 7 (loại vé)

gọi \(x\times100000\text{ là số tiền vé đã tăng}\)
khi đó \(\hept{\begin{cases}\text{Giá vé khi đó là : }100000\times\left(x+4\right)\\\text{số người trên xe khi đó là : }60-10\times x=10\times\left(6-x\right)\end{cases}}\)
khi đó tổng số tiền bán vé thu được là :
\(100000\times\left(x+4\right)\times10\times\left(6-x\right)=1.000.000\times\left(4+x\right)\times\left(6-x\right)\)
\(\le1.000.000\times\left(\frac{4+x+6-x}{2}\right)^2=25.000.000\)
dấu "=" xảy ra khi \(x+4=6-x\Leftrightarrow x=1\)

+) Xếp 4 bạn vào 4 ghế là sự hoán vị của 4 phần tử. Do đó, không gian mẫu là: \(n\left( \Omega \right) = 4!\) ( phần tử)
a) +) Gọi A là biến cố “Bạn Thảo ngồi ghế đầu tiên”
Ghế đầu tiên là ghế của Thảo nên có 1 cách chọn, 3 ghế còn lại xếp tùy ý 3 bạn nên ta có sự hoán vị của 3 phần tử. Theo quy tắc nhân, ta có: \(n\left( A \right) = 1.3!\) ( phần tử)
+) Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{4}\)
b) +) Gọi B là biến cố “Bạn Thảo ngồi ghế đầu tiên và bạn Huy ngồi ghế cuối cùng”.
Ghế đầu tiên của bạn Thảo và ghế cuối cùng của bạn Huy nên có 1 cách chọn cho cả 2 ghế, 2 ghế còn lại xếp tùy ý 2 bạn nên ta có sự hoán vị của 2 phần tử. Theo quy tắc nhân, ta có: \(n\left( B \right) = 1.1.2!\) ( phần tử)
+) Vậy xác suất của biến cố B là: \(P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{1}{{12}}\)