Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Hướng dẫn giải:
Gọi H, K lần lượt là trung điểm của BC và SA.
Dựng đường thẳng d đi qua H và vuông góc với (ABC). Khi đó d//SA.
Trong mặt phẳng (SAH) dựng đường thằng d 1 đi qua K và vuông góc với SA.
Khi đó, d 1 //AH.
Gọi I = d ∩ d 1 tại. Ta có được IA = IB = IC = IS.
Khi đó mặt cầu cần tìm ở đề bài đi qua các điểm A, B, C, S có tâm là I và bán kính là R = IA.
Dễ thấy A H = 1 2 B C = b 2 + c 2 2
và I H = 1 2 S A = a 2 .
Trong ∆ I A H có
Vậy là ta hoàn thành xong bài toán.
Đáp án A
Gọi O là tâm của tam giác đều ABC, khi đó SO là đường cao của hình chóp. Gọi M là trung điểm của BC ta có thể suy ra:
Khi đó ta tính được: 
trong mặt phẳng (SAO), trung trực của SA cắt SO tại I thì I là tâm mặt cầu ngoại tiếp hình chóp. Khi đó ta tính được bán kính của mặt cầu đó là:
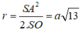
Thể tích khối cầu ngoại tiếp hình chóp là:
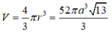
Đáp án D
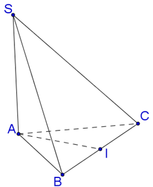
Mặt trụ đi qua hai điểm B,C và có một đường sinh là SA. Vậy mặt trụ đi qua ba điểm A,B,C, nhận đường tròn ngoại tiếp tam giác ABC là đường tròn đáy. Gọi I là trung điểm của BC. Ta suy ra I chính là tâm đường tròn đáy. Bán kính IA = IB = IC = a 2 .
Đáp án D
Gọi O là tâm của tam giác đều ABC. Ta có: SAO ^ = 30o => AO = a 3 => AB = AC = 3a