Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

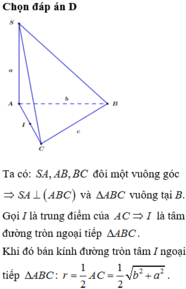
Đáp án D
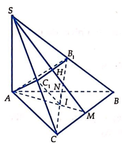
Gọi I là tâm mặt cầu ngoại tiếp hình chóp tam giác S.ABC. Hạ IJ vuông góc với (SAB) . Vì J các đều 3 điểm S; A; B nên J cũng cách đều ba điểm S; A; B
Vì tam giác SAB vuông tại đỉnh S nên J là trung điểm của AB.
Ta có S J = 1 2 A B = 1 2 a 2 + b 2
Do SC vuông góc với (SAB) nên IJ//SC.
Gọi H là trung điểm của SC, ta có S H = I J = c 2
Do vậy I S 2 = I J 2 + S J 2 = a 2 + b 2 + c 2 4 và bán kính hình cầu ngoại tiếp S.ABC là R = I S = 1 2 a 2 + b 2 + c 2

Đáp án A
Giả sử S A → = x S A ' → ; S B → = y S B ' → ; S C → = z S C ' → .
Gọi G là trọng tâm tam giác ABC ⇒ G A → + G B → + G C → = 0 .
⇒ 3 G S → + S A → + S B → + S C → = 0
⇒ S G → = S A → 3 + S B → 3 + S C → 3 ⇒ S G → = x 3 . S A ' → + y 3 . S B ' → + z 3 . S C ' → 1
Do A ' B ' C ' đi qua G nên ba vectơ G A ' → ; G B ' → ; G C ' → đồng phẳng
Suy ra tồn tại 3 số i ; m ; n , i 2 + m 2 + n 2 ≠ 0 sao cho i . G A ' → + m . G B ' → + n . G C ' → = 0
i + m + n . G S → + i . S A ' → + m . S B ' → + n . S C ' → = 0
⇒ S G → = i i + m + n S A ' → + m i + m + n S B ' → + n i + m + n . S C ' → 2
Do S G ; S A ' ; S B ' ; S C ' không đồng phẳng nên từ (1) và (2) ta có
x 3 = i i + m + n ; y 3 = m i + m + n ; z 3 = n i + m + n
x + y + z 3 = i + m + n i + m + n = 1 ⇒ x + y + z = 3
Ta có 1 S A ' 2 + 1 S B ' 2 + 1 S C ' 2 = x 2 a 2 + y 2 b 2 + z 2 c 2
Áp dụng bất đẳng thức Bunyakovsky cho hai bộ số thực x a ; y b ; z c và a ; b ; c ta có .
x 2 a 2 + y 2 b 2 + z 2 c 2 a 2 + b 2 + c 2 ≥ x + y + z 2
⇔ 1 S A ' 2 + 1 S B ' 2 + 1 S C ' 2 ≥ x + y + z 2 a 2 + b 2 + c 2 = 3 a 2 + b 2 + c 2
Dấu “=” xảy ra khi x 2 a 2 = y 2 b 2 = z 2 c 2

Đáp án B.
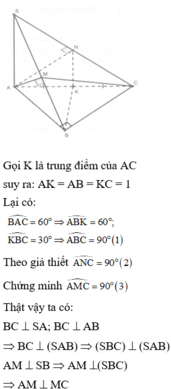
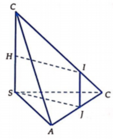
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC ⇒ I A = I B = I C (1).
Ta có ∆ S A C = ∆ S A B ⇒ A B 1 = A C 1 . Từ đây ta chứng minh được B 1 C 1 / / B C .
Gọi M là trung điểm của B C ⇒ B C ⊥ S A M ⇒ B 1 C 1 ⊥ S A M .
Gọi H = S M ∩ B 1 C 1 ⇒ H B 1 M B = H C 1 M C , do M B = M C nên H B 1 = H C 1
Mặt phẳng (SAM) đi qua trung điểm H của B 1 C 1 nên B 1 C 1 ⊥ S A M nên (SAM) là mặt phẳng trung trực của B 1 C 1 . Do I ∈ A M ⊂ S A M nên I B 1 = I C 1 (2).
Gọi N là trung điểm của AB, suy ra A B ⊥ I N S A ⊥ I N ⇒ I N ⊥ S A B .
Tam giác A B B 1 vuông tại B 1 có N là trung điểm của AB nên N A = N B 1 = 1 2 A B .
Như vậy ta có các tam giác vuông sau bằng nhau
∆ I N A = ∆ I N B = ∆ I N B 1 ⇒ I A = I B = I B 1 (3).
Từ (1), (2) và (3) suy ra 5 điểm A,B,C, B 1 , C 1 cùng nằm trên mặt cầu tâm I, bán kính R = I A = 2 3 . a 3 2 = a 3 3 (do ABC là tam giác đều và I là tâm đường tròn ngoại tiếp ⇒ I cũng là trọng tâm tam giác ABC).