Tìm tất cả các giá trị của tham số m để hàm số y = x 3 - m x 2 + 2 m - 3 x - 3 đạt cực đại tại x = 1.
A. m = 3
B. m > 3
C. m ≤ 3
D. m < 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 3 2017
Chọn B.
Đạo hàm: y’ = 3x2 – 2mx + 2m – 3 và y” = 6x – 2m
+ Để hàm số đạt cực đại x = 1 thì:
H
6 tháng 6 2023
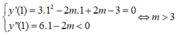
Ta có:
\(y'=x^2-2mx+m^2-4\)
\(y''=2x-2m,\forall x\in R\)
Để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đại tại x = 3 thì:
\(\left\{{}\begin{matrix}y'\left(3\right)=0\\y''\left(3\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2-6m+5=0\\6-2m< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m=1,m=5\\m>3\end{matrix}\right.\Leftrightarrow m=5\)
=> B.
Chọn B
+ Để hàm số đạt cực đại x = 1 thì