Điền số thích hợp vào ô trống:
Trung bình cộng của 5 số lẻ liên tiếp là 45. Vây 5 số viết theo thứ tự từ bé đến lớn lần lượt là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi 3 số lẻ đó là: $x, x+2, x+4$
Tổng của 3 số là:
$x+(x+2)+(x+4)=357\times 3$
$3\times x+6=1071$
$3\times x=1071-6=1065$
$x=1065:3=355$
Vậy số lẻ đầu tiên là $355$, số lẻ tiếp theo là $357, 359$
Trung bình của 5 số chẵn liên tiếp là 302. Tìm 5 số đó:
-5 số đó được viết theo thứ tự từ bé đến lớn


Tổng của hai số tự nhiên đó là:
122×2=244
Ta có sơ đồ:
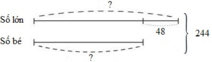
Số lớn là:
(244+48):2=146
Số bé là:
146−48=98
Tích của hai số tự nhiên đó là:
146×98=14308
Đáp số: 14308.
Vậy đáp án đúng điền vào ô trống là 14308.
Chú ý
Học sinh có thể làm sai khi lấy tổng chính bằng số trung bình cộng và bằng 122, sau đó áp dụng công thức tìm được hai số là 85 và 37, từ đó tìm được tích sai là 3145.

Chữ số 6 trong số 609287 nằm ở hàng trăm nghìn nên có giá trị là 600000.
Chữ số 6 trong số 143682 nằm ở hàng chục nên có giá trị là 600.
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là 600000;600.

Số trung bình cộng của các số 27;45 là:
(27+45):2=36
Vậy đáp án đúng điền vào ô trống là 36.
Số trung bình cộng của các số 27 và 45 là:
(27 + 45) : 2 = 36
Đáp số: 36

Để số 38a75 chia hết cho 3 thì tổng các chữ số của số phải chia hết cho 3, hay
(3+8+a+7+5)⋮3
(a+23)⋮3⇒a=1;4;7
Vậy để số 38a75 chia hết cho 3 thì a=1;4;7.
Đáp án đúng điền vào ô trống lần lượt từ trái sang phải là 1;4;7.
Ta có trung bình cộng của một dãy số tự nhiên cách đều có lẻ số (có 3 số, 5 số, 7 số,…) là số ở chính giữa dãy số đó.
Theo đề bài, trung bình cộng của 5 số lẻ liên tiếp là 45 nên dãy số cần tìm có số ở chính giữa hay số thứ ba trong dãy số là 45.
Mà các số trong dãy số là số lẻ nên khoảng cách giữa 2 số liên tiếp là 2 đơn vị.
Số thứ hai trong dãy số là: 45−2=43
Số thứ nhất trong dãy số là: 43−2=41
Số thứ tư trong dãy số là: 45+2=47
Số thứ năm trong dãy số là: 47+2=49
Vậy đáp án đúng cần điền từ trái sang phải, từ trên xuống dưới lần lượt là là: 41;43;45;47;49.