Hạt prôtôn p có động năng K1 = 5,48 MeV được bắn vào hạt nhân B 4 9 e đứng yên thì thấy tạo thành một hạt nhân L 3 6 i và một hạt X bay ra với động năng bằng K2 = 4 MeV theo hướng vuông góc với hướng chuyển động của hạt p tới. Tính vận tốc chuyển động của hạt nhân Li (lấy khối lượng các hạt nhân tính theo đơn vị u gần bằng số khối của nó). Cho 1 u = 931 , 5 MeV/c2.
A. 0 , 824.10 6 m/s
B. 8 , 24.10 6 m/s
C. 10 , 7.10 6 m/s
D. 1 , 07.10 6 m/s

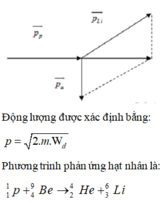
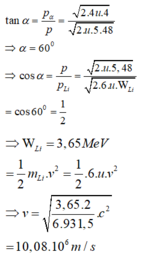
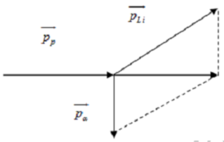
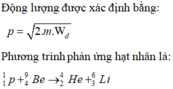
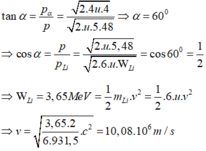
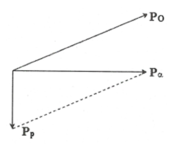
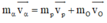
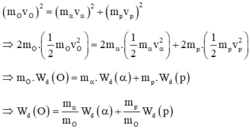
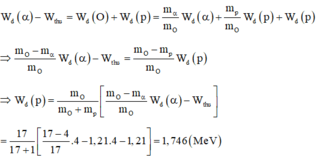
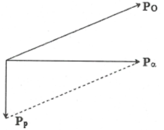

Đáp án C