Hãy chứng minh định lý trên.
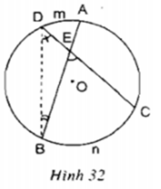
Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
B E C ^ = s d B n C ^ + s d A m D ^ 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



<:góc.
a, Ta có :<ADC = <BAD+<B
<ADB = <CAD+<C
=><ADC-<ADB=(<BAD+<B)-(<CAD+<C)
Mà <BAD=<CAD
=><ADC-<ADB=<B-<C(đpcm)
b,Ta có <BAE=1/2(<B+<C)
<ABE=180o - <B
=><AEB=180o-(180o-<B)-1/2(B+C)
=><AEB=<B-1/2<B-1/2<C
=><AEB=1/2<B+1/2(-<C)
=><ABE=1/2(<B-<C)
Xin lỗi bạn nha!
<AEB=1/2(<B-<C) chứ không phải <ABE đâu

Câu a (1,0đ) Chứng minh :![]() ABD =
ABD = ![]() ACE
ACE
Xét ![]() ABD và
ABD và![]() ACE :có AB=AC (cạnh bên
ACE :có AB=AC (cạnh bên ![]() cân);
cân); ![]() =
=![]() (góc đáy
(góc đáy![]() cân);BD=CE (gt) (0,25đ) x3=(0,75đ)
cân);BD=CE (gt) (0,25đ) x3=(0,75đ)
Vậy ![]() ABD =
ABD = ![]() ACE(cgc) (0,25đ)
ACE(cgc) (0,25đ)
Câu b (0,75đ) Chứng minh đúng ![]() vuông AMD =
vuông AMD = ![]() vuông ANE vì có AD = AE;
vuông ANE vì có AD = AE; ![]()
(do ![]() ABD =
ABD =![]() ACE) (0,5đ)
ACE) (0,5đ)
Kết luận ![]() AMD =
AMD =![]() ANE và suy ra AM =AN) (0,25đ)
ANE và suy ra AM =AN) (0,25đ)
Câu c (0,75đ): Chứng minh đúng ![]() vuông BMD =
vuông BMD =![]() vuông CNE (cạnh huyền - góc nhọn )(0,25đ)
vuông CNE (cạnh huyền - góc nhọn )(0,25đ)
Lập luận chứng minh được ![]() rồi suy ra
rồi suy ra ![]() KDE cân tại K (1)(0,25đ)
KDE cân tại K (1)(0,25đ)
Từ ![]() lập luận để
lập luận để ![]()
![]() (2)
(2)
Kết hợp (1)và (2) ![]()
![]() KDE đều )(0,25đ)
KDE đều )(0,25đ)

Kẻ CH\(\perp\)AB (H\(\in\)AB)
\(\Delta\)BCH vuông tại H có ^B = 600 nên BH = 1/2BC (cạnh đối diện với góc 300 trong tam giác vuông bằng nửa cạnh huyền) hay BC = 2BH
Áp dụng định lý Py-ta-go vào các tam giác AHC và HBC cùng vuông tại H, ta được: AC2 = AH2 + HC2 = (AB - HB)2 + HC2 = AB2 - 2.AB.HB + HB2 + HC2 = AB2 - AB.BC + BC2 (do theo chứng minh trên thì BC = 2BH)
Vậy AC2 = AB2 + BC2 - AB.BC (đpcm)