Trong không gian Oxyz cho mặt cầu S : x − 1 2 + y − 2 2 + z − 3 2 = 9 và mặt phẳng P : 2 x − 2 y + z + 3 = 0. Gọi M a ; b ; c là điểm trên mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Khi đó
A. a + b + c = 6 .
B. a + b + c = 5 .
C. a + b + c = 8 .
D. a + b + c = 7 .





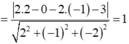
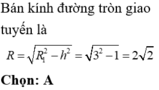



Đáp án D
Tâm I 1 ; 2 ; 3 , R = 3.
Gọi H là hình chiếu của I lên mặt phẳng (P), điểm M cần tìm chính là giao điểm của IH với mặt cầu, M là điểm khác phía với H so với điểm I.
I H : x = 1 + 2 t y = 2 − 2 t z = 3 + t .
Ta tìm giao điểm của IH với mặt cầu (S).
4 t 2 + 4 t 2 + t 2 = 9 ⇔ t = ± 1.
Vậy M 3 ; 0 ; 4 hoặc M - 1 ; 4 ; 2 . Nhận thấy M 3 ; 0 ; 4 có khoảng cách đến (P) lớn hơn.
Vậy a + b + c = 7.