Bạn nào làm đc thì giúp mình nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TB
28 tháng 8 2015
bài 2 a, A1 =180-75=105
D= 75 => D1=105
C=60
B=90
b, A1+B1+C1+D1=105+105+60+90=360
C,tổng các góc ngoài của tứ giác bằng 360
bài 3.
a, AB=AD (GT) nên điểm A thuộc dựng trung trực của BD
CB=AD (GT) nên điểm C thuộc đường trung trực của BD
=> AC là đường trung trực của BD
b,
xét tam giác BAC và DAC
BC=CD
AC
AB=AD
=> tam giác BAC=DAC( ccc)
=> B=D ( 2 GÓC TƯƠNG ỨNG )
trong tứ giác ABCD ; A+B+C+D = 360
=> B+D=200
=> B=D=100 độ
NN
1
E
7
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
V.
\(95^8< 100^8=10^{16}\)
Mà \(10^{16}\) có 17 chữ số nên \(95^8\) có ít hơn 17 chữ số (1)
Lại có: \(95^8>90^8=10^8.9^8=10^8.81^4>10^8.80^4=10^{12}.2^{12}>10^{12}.2^{10}>10^{12}.10^3=10^{15}\)
\(\Rightarrow95^8\) có nhiều hơn 15 chữ số (2)
Từ (1) và (2) \(\Rightarrow95^8\) có 16 chữ số trong cách viết ở hệ thập phân
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
III.
1. Xét hiệu:
\(A-B=\dfrac{2019^{2020}+1}{2019^{2019}+1}-\dfrac{2019^{2019}+1}{2019^{2018}+1}=\dfrac{\left(2019^{2020}+1\right)\left(2019^{2018}+1\right)-\left(2019^{2019}+1\right)^2}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}\)
\(=\dfrac{2019^{4028}+1+2019^{2020}+2019^{2018}-2019^{4028}-2.2^{2019}-1}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}\)
\(=\dfrac{2019^{2020}-2019^{2019}+2019^{2018}-2019^{2019}}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}\)
\(=\dfrac{2019^{2019}\left(2019-1\right)-2019^{2018}\left(2019-1\right)}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}\)
\(=\dfrac{2018.2019^{2019}-2018.2019^{2018}}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}=\dfrac{2018.2019^{2018}\left(2019-1\right)}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}\)
\(=\dfrac{2018^2.2019^{2018}}{\left(2019^{2019}+1\right)\left(2019^{2018}+1\right)}>0\)
\(\Rightarrow A>B\)
NN
1
20 tháng 8 2021
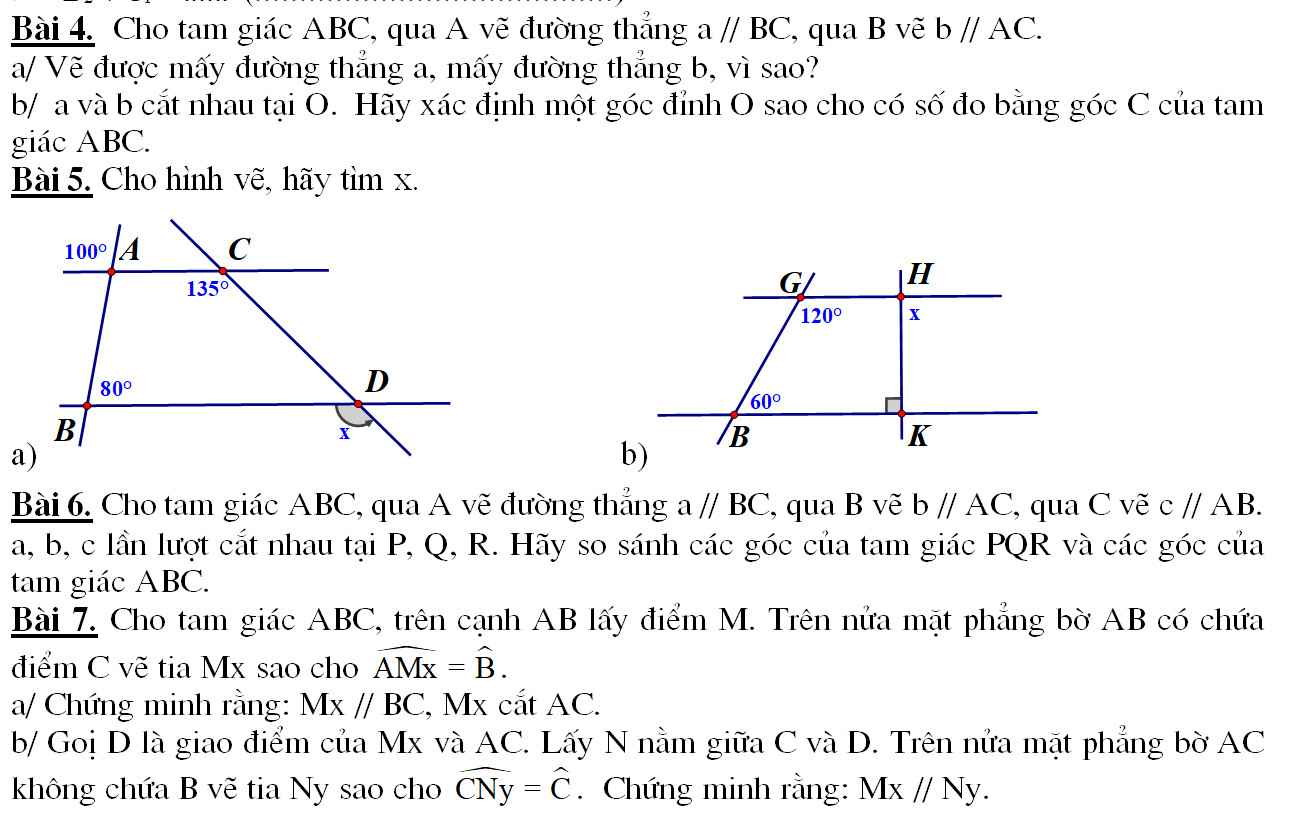
Bài 5:
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
b)
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)
S
cứu mình ạ. Nhanh đc thì tốt!!! CẢM ƠN. Bạn nào mà giúp mình đc thì thi toán sẽ đc điểm tốt nha!! <3
0
B
19 tháng 6 2023
1 Would you mind lending me some books?
2 Old car tires are recycled to make shoes and sandals.
3 The man who is sitting on the chair is my father.
4 They passed the final exam so they are very happy.
LN
2
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
3.
Do \(sin\left(x+k2\pi\right)=sinx\Rightarrow sin\left(x+2020\pi\right)=sinx\)
\(sin\left(\dfrac{\pi}{2}+x\right)=cos\left(\dfrac{\pi}{2}-\dfrac{\pi}{2}-x\right)=cos\left(-x\right)=cosx\)
\(A=\dfrac{sinx+sin3x+sin5x}{cosx+cos3x+cos5x}=\dfrac{sinx+sin5x+sin3x}{cosx+cos5x+cos3x}\)
\(=\dfrac{2sin3x.cosx+sin3x}{2cos3x.cosx+cos3x}=\dfrac{sin3x\left(2cosx+1\right)}{cos3x\left(2cosx+1\right)}\)
\(=\dfrac{sin3x}{cos3x}=tan3x\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
4.
a.
\(\overrightarrow{CB}=\left(2;-2\right)=2\left(1;-1\right)\)
Do đường thẳng d vuông góc BC nên nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình đường thẳng d đi qua \(A\left(-1;2\right)\) và có 1 vtpt là \(\left(1;-1\right)\) là:
\(1\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow x-y+3=0\)
b.
Gọi \(I\left(a;b\right)\) là tâm đường tròn, ta có \(\left\{{}\begin{matrix}\overrightarrow{AI}=\left(a+1;b-2\right)\\\overrightarrow{BI}=\left(a-3;b-2\right)\\\overrightarrow{CI}=\left(a-1;b-4\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AI^2=\left(a+1\right)^2+\left(b-2\right)^2\\BI^2=\left(a-3\right)^2+\left(b-2\right)^2\\CI^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
Do I là tâm đường tròn qua 3 điểm nên: \(\left\{{}\begin{matrix}AI=BI\\AI=CI\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}AI^2=BI^2\\AI^2=CI^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a+1\right)^2+\left(b-2\right)^2=\left(a-3\right)^2+\left(b-2\right)^2\\\left(a+1\right)^2+\left(b-2\right)^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8a=8\\4a+4b=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\) \(\Rightarrow I\left(1;2\right)\)
\(\overrightarrow{AI}=\left(2;0\right)\Rightarrow R=AI=\sqrt{2^2+0^2}=2\)
Pt đường tròn có dạng:
\(\left(x-1\right)^2+\left(y-2\right)^2=4\)
