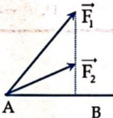
Một vật chịu tác dụng của lần lượt hai lực khác nhau F1 > F2 và cùng đi được quãng đường trên phương AB như hình vẽ sinh công tương ứng là A1 và A2. Hệ thức đúng là
A. A1 > A2
B. A1 < A2
C. A1 = A2
D. A1 A2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Theo công thức tính công ta có: A = F.S.cos α = F.cosα.S = F S S (*)
+ F S chính là độ dài đại số hình chiếu của lực F lên phương của quỹ đạo chuyển động S
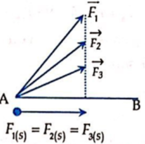
+ Theo hình ta có: F 1 S = F 2 S = F 3 S
+ Mặt khác theo bài: S 1 = S 2 = S 3 = AB
+ Do vậy từ (*) ta suy ra: A 1 = A 2 = A 3

Theo công thức tính công ta đã xây dựng được công thức bổ đề:
![]()
+ Fs chính là độ dài đại số hình chiếu của lực F lên phương của quỹ đạo chuyển động S

Áp dụng định luật ll Niu-tơn:
\(F_1=m\cdot a_1\)
\(F_2=m\cdot a_2\)
\(\Rightarrow\dfrac{F_2}{F_1}=\dfrac{a_2}{a_1}\)
Mà \(3F_1=2F_2\Rightarrow\dfrac{F_2}{F_1}=\dfrac{3}{2}=\dfrac{a_2}{a_1}\)
Chọn D.

Đáp án D
Với ![]() => Với
=> Với ![]() thì
thì ![]()
Ta luôn có ![]() => không thể là 0,5m/
s
2
=> không thể là 0,5m/
s
2


\(\overrightarrow{A}=\overrightarrow{A_1}+\overrightarrow{A_2}\)
Định lý hàm sin: \(\dfrac{A}{\sin\dfrac{\pi}{6}}=\dfrac{A_2}{\sin\alpha}=\dfrac{A_1}{\sin\beta}\)
\(A_2\left(max\right)\Rightarrow\sin\alpha_{max}=1\Rightarrow\left\{{}\begin{matrix}A_2=\dfrac{9}{\dfrac{1}{2}}=18\left(cm\right)\\\alpha=\dfrac{\pi}{2}\left(rad\right)\end{matrix}\right.\)
\(\Rightarrow\beta=\pi-\dfrac{\pi}{6}-\dfrac{\pi}{2}=\dfrac{\pi}{3}\left(rad\right)\Rightarrow A_1=18.\sin\dfrac{\pi}{3}=9\sqrt{3}\left(cm\right)\)
Theo công thức tính công ta đã xây dựng được công thức bổ đề:
+ chính là độ dài đại số hình chiếu của lực lên phương của quỹ đạo chuyển động S