Sau khi rút gọn biểu thức 2 7 + 3 5 + 2 7 - 3 5 ta được phân số tối giản a b , (a, b ∈ ℤ ). Khi đó a+b có giá trị là:
A. 28
B. 7
C. 8
D. 14
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

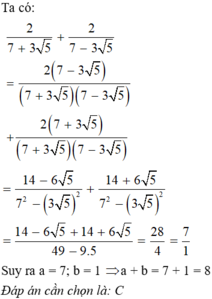

Tử số a là: 18:(7-5)*5=45
Mẫu số b là:45+18=63
Phân số \(\frac{a}{b}\)là \(\frac{45}{63}\)

`(2-2/5+6/5)-(3/15+2)+(7/3-2)`
`=2+4/5-3/15-2-2+7/3`
`=-2+4/5-1/5+7/3`
`=-2+3/5+2+1/3`
`=3/5+1/3=14/15`
`=>a=14,b=15`
`=>S=2.14-15=13`

ta có
\(\frac{a}{b}=\frac{5}{11}\Leftrightarrow\frac{b-a}{b}=\frac{11-5}{11}\Leftrightarrow\frac{18}{b}=\frac{6}{11}\)
Vậy \(b=33\Rightarrow a=33-18=15\) hay \(\frac{a}{b}=\frac{15}{33}\)

1) Các phân số tối giản là: \(\frac{1}{5};\frac{5}{7};\frac{-2}{9}\)
2) a) \(\frac{28}{36}=\frac{28:4}{36:4}=\frac{7}{9}\)
b) \(\frac{-63}{90}=\frac{-63:9}{90:9}=\frac{-7}{10}\)
c) \(\frac{40}{-120}=\frac{40:40}{-120:40}=\frac{-1}{3}\)
3) a) \(\frac{2.4}{6.18}=\frac{2.2.2}{2.3.3.2.3}=\frac{2}{27}\)
b) \(\frac{3.5.7}{6.9.14}=\frac{3.5.7}{2.3.9.2.7}=\frac{5}{36}\)
c) \(\frac{4.7-4.5}{64}=\frac{4.\left(7-5\right)}{64}=\frac{4.2}{64}=\frac{8}{64}=\frac{1}{8}\)
4) Muốn rút gọn một phân số chưa tối giản, ta tìm ƯCLN của cả hai số ở tử và mẫu, rồi cùng đem cả tử và mẫu chia cho số chung vừa tìm được.

a. Mẫu số chung nhỏ nhất là 24
b. \(\dfrac{5}{7}\)
c. \(\dfrac{3}{4}\)
d. \(\dfrac{9}{12}\) và giữ nguyên phân số còn lại
e. \(\dfrac{3}{6};\dfrac{4}{6};\dfrac{5}{6}\)
g. \(\dfrac{9}{12};\dfrac{4}{12};\dfrac{2}{12}\)
h. \(\dfrac{15}{60};\dfrac{20}{60};\dfrac{12}{60}\)
i. \(\dfrac{10}{1}\)