Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.
a) So sánh MB + MC với BC
b) Chứng minh M A + M B + M C > A B + B C + C A 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

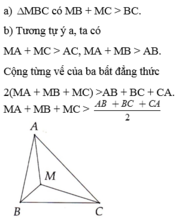

a) Xét ΔBMC ta có: MB + MC > BC (bất đẳng thức tam giác)
b)
*Xét ΔABM ta có: AM + BM > AB (1)
*Xét ΔACM ta có: AM + CM > AC (2)
*Xét ΔBMC ta có: BM + CM > BC (3)
Từ (1); (2); (3)
=> AM + BM + AM + CM + BM + CM > AB + AC + BC
=> 2. AM + 2. BM + 2. CM > AB + AC + BC
=> 2. (AM + BM + CM) > AB + AC + BC
Hay: 2. (MA + MB + MC) > AB + BC + CA
c)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
d)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
e)Từ (2) và (4) suy ra MB+MC<AB+AC
f)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)

a) Xét ΔBMC ta có: MB + MC > BC (bất đẳng thức tam giác)
b)
*Xét ΔABM ta có: AM + BM > AB (1)
*Xét ΔACM ta có: AM + CM > AC (2)
*Xét ΔBMC ta có: BM + CM > BC (3)
Từ (1); (2); (3)
=> AM + BM + AM + CM + BM + CM > AB + AC + BC
=> 2. AM + 2. BM + 2. CM > AB + AC + BC
=> 2. (AM + BM + CM) > AB + AC + BC
Hay: 2. (MA + MB + MC) > AB + BC + CA
c)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
d)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
e)Từ (2) và (4) suy ra MB+MC<AB+AC
f)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)

a)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
b)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
c)Từ (2) và (4) suy ra MB+MC<AB+AC
d)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)

cho tam giác ABC và M là một điểm bất kỳ nằm trong tam giác đó.C/m MA+MB+MC
a/lớn hơn nửa chu vi tam giác đó
b/nhỏ hơn chu vi tam giác ABC
Câu hỏi tương tự Đọc thêmToán lớp 7Hình học