Cho tứ diện ABCD. M, N lần lượt là trọng tâm của các tam giác ABC, ABD. Thiết diện của tứ diện với mặt phẳng (∝) chứa MN và song song với AB là hình gì?
A. tam giác
B. hình bình hành
C. hình thoi
D. hình thang có đúng một cặp cạnh song song
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
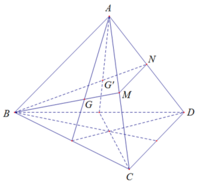
Trong(ABC), ta có: BG cắt AC tại M
Trong (ABD), ta có: BG’ cắt AD tại N
⇒ (BGG’) ∩ (ACD) = MN
Thiết diện cần tìm là (BMN)
Xét tam giác BMN có:
MN = 1 2 CD = a 2 ( MN là đường trung bình của tam giác ACD)
BM = BN = a 3 2 (BM, BN lần lượt là đường trung tuyến của tam giác ABC, ABD)
Áp dụng công thức heron:
S = p p - a p - b p - c = a 2 11 6

a) Do các tứ giác ABCD và ABEF là các hình bình hành
=> O là trung điểm của AC và BD
và O’ là trung điểm của AE và BF. (tính chất hình bình hành).
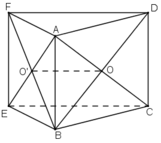
+ ΔBFD có OO’ là đường trung bình nên OO’ // DF
mà DF ⊂ (ADF)
⇒ OO' // (ADF)
+ ΔAEC có OO’ là đường trung bình nên OO’ // EC
mà EC ⊂ (BCE)
⇒ OO’ // (BCE).
b)
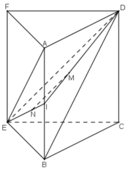
Ta thấy mp(CEF) chính là mp(CEFD).
Gọi I là trung điểm của AB:
+ M là trọng tâm ΔABD
⇒ IM/ ID = 1/3.
+ N là trọng tâm ΔABE
⇒ IN/IE = 1/3.
+ ΔIDE có IM/ID = IN/IE = 1/3
⇒ MN // DE mà ED ⊂ (CEFD)
nên MN // (CEFD) hay MN // (CEF).
(∝) // AB nên giao tuyến của (∝) với (ABC) là đường thẳng qua M, song song với AB, cắt BC tại Q, cắt AC tại G
(∝) // AB nên giao tuyến của (∝) với (ABC) là đường thẳng qua N, song song với AB, cắt BD tại P, cắt AD tại F
Gọi E là trung điểm của AB. M, N lần lượt là trọng tâm các tam giác ABC, ABD nên
theo định lí Ta- lét ta có MN // CD.
Do MN // CD nên PQ // GF // CD, lại có QG // FP(//AB nên thiết diện là hình bình hành GQPF.
Đáp án B