Cho hình lập phương ABCD.A’B’C’D’: Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:
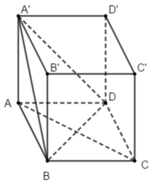
A. trung điểm của BD
B. trung điểm của A’B
C. trung điểm của A’D
D. tâm của tam giác BDA’
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 11 2017
Chọn đáp án D
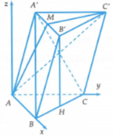
Gọi H là trung điểm của cạnh BC. Suy ra B ' H ⊥ A B C
∆ A B C vuông tại A nên B C = A B 2 + A C 2 = 5
vuông tại H nên B ' H = B ' B 2 - B H 2 = 3
Chọn hệ trục tọa độ Oxyz như hình, trong đó A ≡ O 0 ; 0 ; 0 , B 3 ; 0 ; 0 , C 0 ; 4 ; 0 .
Ta có H là trung điểm của BC nên H 3 2 ; 2 ; 0 , H là hình chiếu của B’ trên bề mặt phẳng (ABC) nên B ' 3 2 ; 2 ; 3 .
Từ A B ⇀ = A ' B ' ⇀ suy ra
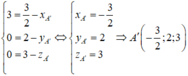
Từ A C ⇀ = A ' C ' ⇀ suy ra
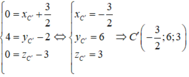
M là trung điểm của A’B’ nên M(0;2;3).
Ta có
Mặt phẳng (AMC’) có một vectơ pháp tuyến là n 1 ⇀ = 8 ; 3 ; - 2 .
Lại có A ' B ⇀ = 9 2 ; - 2 ; - 3 , A ' C ⇀ = 3 2 ; 2 ; - 3
⇒ A ' B ⇀ , A ' C ⇀ = 12 ; 9 ; 12
⇒ Mặt phẳng (A’BC) có một vectơ pháp tuyến là n 2 ⇀ = 4 ; 3 ; 4 .
Gọi α là góc tạo bởi hai mặt phẳng (AMC’) và (A’BC) thì:
⇒ cos α = 33 3157
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
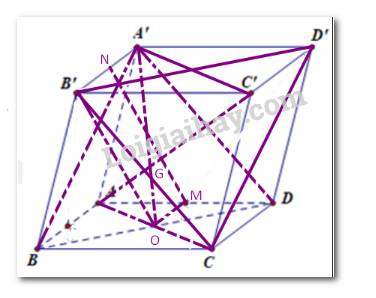
a) Ta có: (ABCD) // (A’B’C’D’)
\(\left( {B'D'DB} \right) \cap \left( {A'B'C'D'} \right) = B'D',\)
\(\left( {B'D'DB} \right) \cap \left( {ABCD} \right) = BD\).
Suy ra B'D' // DB.
Xét (A'BD) và (CB'D') có BD // B'D', A'B // CD'.
Suy ra (A'BD) //(CB'D').
Xét tứ giác B'NMO ta có: B'N = MO, B'N // MO.
Suy ra B'NMO là hình bình hành.
Suy ra B'O // MN hay MN // (BDD'B').
b) Xét tứ giác A'C'OA ta có: A'C' // AO, A'C' = 2AO
Suy ra A'G =2GO.
Mà O là trung điểm BD.
Suy ra G là trọng tâm tam giác A'BD.
Như vậy AC' đi qua trọng tâm G của tam giác A'BD.
CM
16 tháng 1 2019
Đáp án D
Phương pháp:
Thể tích hình hộp trong đó:
B: diện tích đáy,
h: chiều cao
Cách giải:
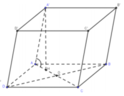
Do AA’ // CC’ nên (AA’,ABCD) = (CC’,ABCD) = 600
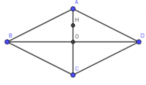
Hình thoi ABCD có AB = CD = BC = DA = a. BD= B'D' = a 3
Tam giác OAB vuông tại O:
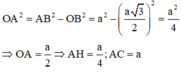
Diện tích hình thoi ABCD: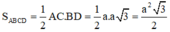 
Tam giác A’AH vuông tại H:
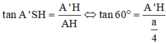
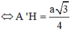
Thể tích hình hộp ABCD.A’B’C’D’:
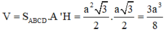
Ta có: BD = A’B = A’D nên tam giác A’BD là tam giác đều.
Lại có: AB = AD = AA’ nên hình chiếu vuông góc của điểm A lên mp(A’BD) là tâm của tam giác BDA’.
Đáp án D