Tìm trên đường thẳng x = 3 điểm M có tung độ là số nguyên nhỏ nhất mà qua đó có thể kẻ tới đồ thị (C) của hàm số y = x 3 - 3 x 2 + 2 đúng 3 tiếp tuyến phân biệt.
A. M(3;2)
B. M(3;-6)
C. M(3;1)
D. M(3;-5)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 6 2019
Đáp án D.
y ' = 3 x 2 − 12 x + 9
Gọi M x 0 ; x 0 3 − 6 x 0 2 + 9 x 0 − 1 là một điểm bất kì thuộc (C) . Tiếp tuyến tại M:
y = 3 x 0 2 − 12 x 0 + 9 x − x 0 + x 0 3 − 6 x 0 2 + 9 x 0 − 1
⇔ y = 3 x 0 2 − 12 x 0 + 9 x − 2 x 0 3 + 6 x 0 2 − 1
Gọi A a ; a − 1 là một điểm bất kì thuộc đường thẳng y = x − 1 .
Tiếp tuyến tại M đi qua A ⇔ 3 x 0 2 − 12 x 0 + 9 a − 2 x 0 3 + 6 x 0 2 − 1 = a − 1
⇔
3
x
0
2
−
12
x
0
+
8
a
=
2
x
0
3
−
6
x
0
2
(*).
Từ A kẻ được hai tiếp tuyến đến C ⇔ * có hai nghiệm phân biệt.
Ta có
3 x 0 2 − 12 x 0 + 8 = 0 ⇔ x 0 = 6 ± 2 3 3
Dễ thấy x 0 = 6 ± 2 3 3 không thỏa mãn .
Với x 0 ≠ 6 ± 2 3 3 thì * ⇔ a = 2 x 0 3 − 6 x 0 2 3 x 0 2 − 12 x 0 + 8 .
Xét hàm số f x = 2 x 3 − 6 x 2 3 x 2 − 12 x + 8 . Ta có f ' x = 6 x 4 − 8 x 3 + 20 x 2 − 16 x 3 x 2 − 12 x + 8 2 .
Bảng biến thiên của :
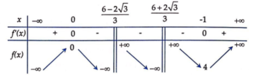
Vậy để (*) có 2 nghiệm phân biệt thì a ∈ 0 ; 4 . Suy ra tập T = 0 ; − 1 , 4 ; 3
Do đó tổng tung độ các điểm thuộc T bằng 2.
27 tháng 4 2016
Xét \(M\left(0;m\right)\in Oy\). Đường thẳng d đi qua M, hệ số góc k có phương trình : \(y=kx+m\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}x^4-2x^2-1=kx+m\\4x^3-4x=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(-x^4-2x^2-1=4x^4-4x^2+m\)
\(\Leftrightarrow5x^4-2x^2+1+m=0\) (*)
Để từ M ta có thể kẻ đến đồ thị đúng 3 tiếp tuyến \(\Leftrightarrow\) (*) có 3 nghiệm phân biệt \(\Leftrightarrow m+1=0\Leftrightarrow m=-1\)
Khi đó (*) có 3 nghiệm \(x=0;x=\pm\sqrt{\frac{2}{5}}\) và 3 tiếp tuyến đó là :
\(y=-1;y=\pm\sqrt{\frac{2}{5}}x-1\)
Vậy \(M\left(0;-1\right)\) là điểm cần tìm
KT
6 tháng 1 2019
Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
KT
6 tháng 1 2019
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)
Đáp án D