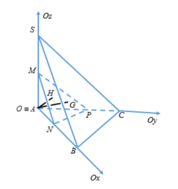
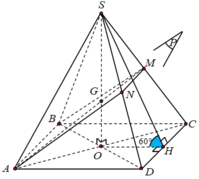
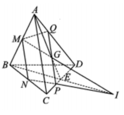
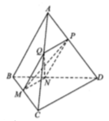
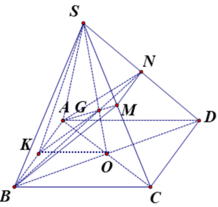
Cho tứ diện đều S.ABC có cạnh bằng 1. Mặt phẳng (P) đi qua điểm S và trọng tâm G của tam giác ABC cắt các cạnh AB, AC lần lượt tại M, N. Tính thể tích nhỏ nhất V m i n của khối tứ diện SAMN.
A. V min = 2 27
B. V min = 4 9
C. V min = 2 18
D. V min = 2 36

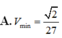
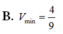
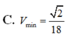
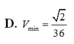

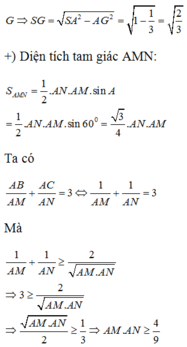
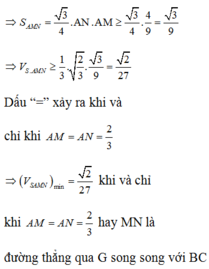
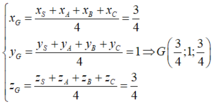
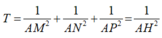
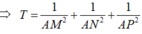
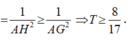

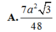
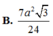
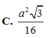
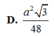


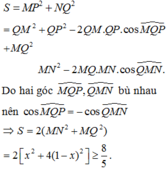
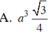
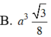
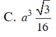
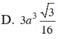
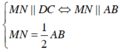
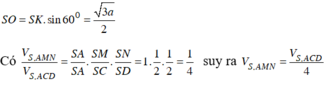
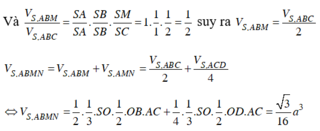
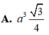
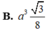

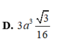

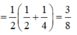

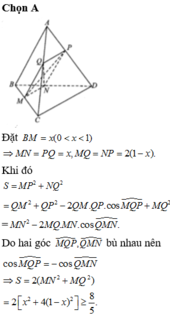
Chọn A.
Phương pháp:
Cho tam giác đều ABC, G là trọng tâm tam giác ABC. Đường thẳng qua G cắt AB, AC lần lượt tại M, N. Khi đó,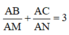
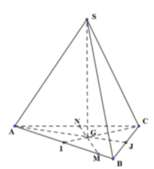
Thật vậy, gọi I là trung điểm của BC, qua B, C kẻ các đường thẳng song song MN, cắt đường thẳng AI tại E, F.
Cách giải:
Do SABC là tứ diện đều, G là trọng tâm tam giác ABC