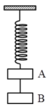
Hai vật có khối lượng m 1 = 800 g , m 2 = 600 g được nối với nhau bằng dây ko dãn như hình vẽ, lúc đầu hai vật đứng yên. Khi thả ra vật hai chuyển động được 50cm thì vận tốc của nó là v = 1 ( m / s ) . Biết m1 trượt trên mặt phẳng nghiêng góc α = 30 0 so với phương nằm ngang và có hệ số ma sát . Tính hệ số ma sát μ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có P 1 x = P 1 . sin 30 0 = m 1 g . 1 2 = 0 , 15.10.0 , 5 = 0 , 75 ( N ) P 2 = m 2 g = 0 , 1.10 = 1 ( N )
Vậy P 2 > P 1 x vật hai đi xuống vật một đi lên, khi vật hai đi xuống được một đoạn s = 1m thì vật một lên cao z 1 = s . sin 30 0 = s 2 = 0 , 5 ( m )
Chọn vị trí ban đầu của hai vật là mốc thế năng
Theo định luật bảo toàn năng lượng
0 = W d + W t + A m s
W d = ( m 1 + m 2 ) v 2 2 = ( 0 , 15 + 0 , 1 ) v 2 2 = v 2 8 W t = − m 2 g s + m 1 g z 1 = − 0 , 1.10.1 + 0 , 15.10.0 , 5 = − 0 , 25 ( J ) A m s = F m s . s = μ m 1 g . cos 30 0 . s = 0 , 1.0 , 15.10. 3 2 .1 = 0 , 1299 ( J ) 0 = v 2 8 − 0 , 25 + 0 , 1299 ⇒ v ≈ 0 , 98 ( m / s )

Đáp án C
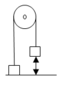
Dễ thấy rằng, vật B ngay sau khi dây nối bị cắt sẽ rơi tự do với gia tốc g.
Vật A ngay sau khi dây đứt sẽ dao động điều hòa quanh vị trí cân bằng mới, vị trí này nằm trên vị trí cân bằng cũ một đoạn △ l = m g k .
Mặc khác vị trí sau khi cắt dây của A cũng là vị trí biên → a = a m a x = ω 2 A = 0,5g

Đáp án B
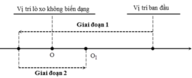
Nhận thấy rằng, lực ma sát trượt giữa M và m chỉ tồn tại khi dây D căng → tương ứng với chuyển động của m về phía bên trái. Do vậy ta có thể chia quá trình chuyển động của m thành các giai đoạn sau:
Giai đoạn 1: Dao động tắt dần quanh vị trí cân bằng tạm O 1
+ Tại vị trí cân bằng tạm, lực đàn hồi cân bằng với lực ma sát k Δ l 0 = μ M g → Δ l 0 = μ M g k = 0 , 2.0 , 3.10 40 = 1 , 5 c m
→ Biên độ dao động trong giai đoạn này là A1 = 4,5 – 1,5 = 3 cm.
+ Vật chuyển động đến biên thì đổi chiều lúc này lò xo bị nén một đoạn Δl = 3 – 1,5 = 1,5 cm.
Thời gian tương ứng trong giai đoạn này t 2 = T 2 2 = π m + M k = π 0 , 1 + 0 , 3 40 = 0 , 1 π s
Giai đoạn 2: m đổi chiều chuyển động → dây chùng không còn ma sát trượt nữa → hệ hai vật m + M dao động điều hòa quanh vị trí cân bằng O (vị trí lò xo không biến dạng)
+ Biên độ dao động của vật ở giai đoạn này A 2 = 1 , 5 c m (biên độ này nhỏ hơn A 2 m a x = μ g ω 2 2 = 2 cm để M không trượt trong quá trình dao động).
Thời gian tương ứng đến khi vật đổi chiều lần thứ hai t 1 = T 1 2 = π m k = π 0 , 1 40 = 0 , 05 π s
→ Tốc độ trung bình của m trong hai giai đoạn trên v t b = S t = 2 A 1 + 2 A 2 t 1 + t 2 = 2 3 + 1 , 5 0 , 05 π + 0 , 1 π = 19 , 1 c m / s

Chọn C.
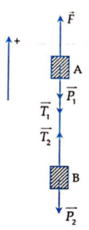
Các lực tác dụng lên hai vật như hình vẽ:
Do dây nhẹ, không dãn nên
T1 = T2 = T; a1 = a2 = a
Chọn chiều dương hướng lên.
Áp dụng đinh luật II Niu-tơn cho từng vật:
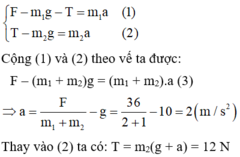

Chọn C.
Các lực tác dụng lên hai vật như hình vẽ:
Do dây nhẹ, không dãn nên T1 = T2 = T; a1 = a2 = a
Chọn chiều dương hướng lên.
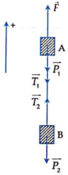

Cộng (1) và (2) theo vế ta được:
F – (m1 + m2)g = (m1 + m2).a (3)
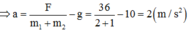
Thay vào (2) ta có: T = m2(g + a) = 12 N

Đáp án B
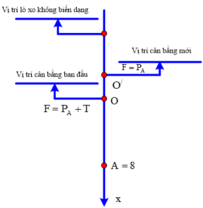
Khi dây chưa bị đứt:
+ Tại VTCB, vật B chịu tác dụng của 3 lực: Trọng lực, lực căng dây và lực điện → Fđ + T = mBg
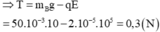
+ Tại VTCB, vật A chịu tác dụng của 3 lực là trọng lực, lực đàn hồi và lực căng dây.
→ Độ biến dạng của lò xo tại vị trí cân bằng O của vật A
![]()
Ban dầu giữa vật A đứng yên sao cho lò xo không biến dạng thả nhẹ vật A → Vật A sẽ dao động điều hòa quanh O với biên độ A = 8cm
Khi vật A đến biên A = 8cm:
Dây bị đứt, vật A sẽ dao động điều hòa quanh vị trí cân bằng mới O’, với O’ cách vị trí lò xo không biên dạng một đoạn ![]()
![]()
![]()
Khoảng cách giữa hai vật khi vật A đi đến vị trí cân bằng mới lần đầu tiên (ứng với 0,25T)

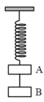

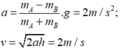
Ta có P 1 x = P 1 . sin 30 0 = m 1 g . 1 2 = 0 , 8.10.0 , 5 = 4 ( N ) P 2 = m 2 g = 0 , 6.10 = 6 ( N )
Vậy P 2 > P 1 x vật hai đi xuống vật một đi lên, khi vật hai đi xuống được một đoạn s = 50 cm thì vật một lên cao
z 1 = s . sin 30 0 = s 2 = 25 ( c m )
Chọn vị trí ban đầu của hai vật là mốc thế năng
Theo định luật bảo toàn năng lượng
0 = W d + W t + A m s V ớ i W d = ( m 1 + m 2 ) v 2 2 = ( 0 , 8 + 0 , 6 ) .1 2 2 = 0 , 7 ( J ) A m s = F m s . s = μ m 1 g . cos 30 0 . s = μ .0 , 8.10. 3 2 .0 , 5 = μ 2 3 ( J )
Vậy 0 = 0 , 7 − 1 + μ .2. 3 ⇒ μ = 0 , 0866