Trong không gian Oxyz, viết phương trình đường thẳng Δ song song với trục Oz và cắt hai đường thẳng d : x 1 = y − 1 2 = z − 6 3 ; d ' : x - 1 1 = y + 2 1 = z − 3 - 1 .
A. Δ : x = 2 y = 5 z = 12 + t
B. Δ : x = - 2 y = - 5 z = 12 + t
C. Δ : x = − 4 y = − 7 z = − 6 + t
D. Δ : x = 4 y = 7 z = − 6 + t

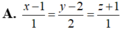
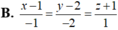

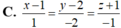
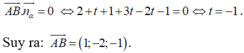
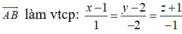
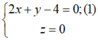
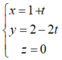
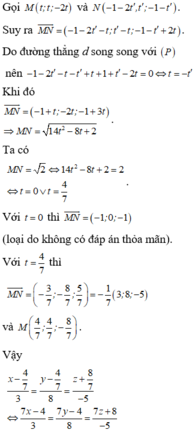

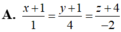
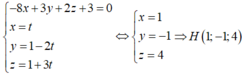

Đáp án C.