Giải phương trình giúp em với ạ, em đang cần gấp ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1:
a, \(\dfrac{2}{3}\) + \(\dfrac{1}{5}\). \(\dfrac{10}{7}\)
= \(\dfrac{2}{3}\) + \(\dfrac{2}{7}\)
= \(\dfrac{20}{21}\)
b, \(\dfrac{7}{12}\) - \(\dfrac{27}{7}\). \(\dfrac{1}{18}\)
= \(\dfrac{7}{12}\) - \(\dfrac{3}{14}\)
= \(\dfrac{31}{84}\)
c, \(\dfrac{3}{10}\). \(\dfrac{-5}{6}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{1}{4}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{3}{8}\)
d, - \(\dfrac{4}{9}\): \(\dfrac{8}{3}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{6}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{9}\)
e, {[(\(\dfrac{1}{2}\) - \(\dfrac{2}{3}\))2 : 2 ] - 1}. \(\dfrac{4}{5}\)
= {[ (-\(\dfrac{1}{6}\))2 : 2] - 1}. \(\dfrac{4}{5}\)
= { [\(\dfrac{1}{36}\) : 2] - 1}. \(\dfrac{4}{5}\)
= { \(\dfrac{1}{72}\) - 1}. \(\dfrac{4}{5}\)
=- \(\dfrac{71}{72}\).\(\dfrac{4}{5}\)
= -\(\dfrac{71}{90}\)

Câu 1:
\(\left\{{}\begin{matrix}y-2x< =2\\2y-x>=4\\x+y< =5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y< =2x+2\\2y>=x+4\\y< =-x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y< =2x+2\\y< =-x+5\\y>=\dfrac{1}{2}x+2\end{matrix}\right.\)
y<=2x+2
=>y-2x-2<=0
Vẽ đường thẳng y=2x+2
Khi x=0 và y=0 thì \(y-2x-2=0-0-2=-2< =0\)(đúng)
=>Miền nghiệm của BPT y<=2x+2 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y<=-x+5
=>x+y-5<=0
Khi x=0 và y=0 thì \(x+y-5=0+0-5< =0\)(đúng)
=>Miền nghiệm của BPT y<=-x+5 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y>=1/2x+2
=>\(-\dfrac{1}{2}x+y-2>=0\)
Khi x=0 và y=0 thì \(-\dfrac{1}{2}x+y-2=-\dfrac{1}{2}\cdot0+0-2=-2< 0\)
=>O(0;0) không thỏa mãn BPT \(-\dfrac{1}{2}x+y-2>=0\)
=>Miền nghiệm của BPT \(y>=\dfrac{1}{2}x+2\) là nửa mặt phẳng chứa biên nhưng không chứa điểm O(0;0)
Vẽ đồ thị:
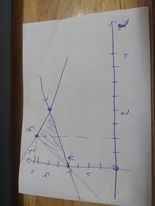
Theo hình vẽ, ta có: Miền nghiệm của hệ BPT sẽ là ΔABC, với A(0;2); B(1;4); C(2;3)
Khi x=0 và y=2 thì F=2-0=2
Khi x=1 và y=4 thì F=4-1=3
Khi x=2 và y=3 thì F=3-2=1
=>Chọn A

1) ĐKXĐ: \(x\ge0\)
2) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
3) ĐKXĐ: \(x\ge4\)
4) ĐKXĐ: \(x>16\)
5) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge0\end{matrix}\right.\)
6) ĐKXĐ: \(\left[{}\begin{matrix}x\le-1\\x\ge4\end{matrix}\right.\)
7) ĐKXĐ: \(\left[{}\begin{matrix}1\le x\\x< 3\end{matrix}\right.\)
8) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x>3\end{matrix}\right.\)
9) ĐKXĐ: \(x\in R\)
10) ĐKXĐ: \(x\in R\)
11) ĐKXĐ: \(x\in R\)
12) ĐKXĐ: \(x\in R\)
13) ĐKXĐ: \(x\in R\)
14) ĐKXĐ: \(x\in R\)
15) ĐKXĐ: \(x\in R\)
16) ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
17) ĐKXĐ: \(x\ge7\)
18) ĐKXĐ: \(x\ge-5\)

\(1,\Leftrightarrow x^2-8x+16-x^2+x+12=7\\ \Leftrightarrow-7x=-21\\ \Leftrightarrow x=3\\ 2,\Leftrightarrow\left(x-4\right)^2-\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)

\(1,\\ a,\dfrac{8x}{2xy}=\dfrac{4x}{y}\\ b,\dfrac{2xy}{6y}=\dfrac{x}{3}\\ c,\dfrac{3\left(x+2\right)}{2x}=\dfrac{6\left(x+2\right)}{4x}\\ d,\dfrac{4\left(x-2\right)}{3\left(x+1\right)}=\dfrac{8\left(x-2\right)x}{6\left(x+1\right)x}\\ 2,\\ \dfrac{x^2+3x+2}{x^2+x}=\dfrac{x^2+x+2x+2}{x\left(x+1\right)}=\dfrac{\left(x+1\right)\left(x+2\right)}{x\left(x+1\right)}=\dfrac{x+2}{x}\\ 3,\\ \dfrac{x^2-3x}{x^2-9}=\dfrac{x}{x+3}\)

Bài 3:
Ta có: \(x^2-2x+4=\left(x-1\right)^2+3\ge3\forall x\)
\(\Leftrightarrow P=\dfrac{15}{x^2-2x+4}=\dfrac{15}{\left(x-1\right)^2+3}\le5\forall x\)
Dấu '=' xảy ra khi x=1
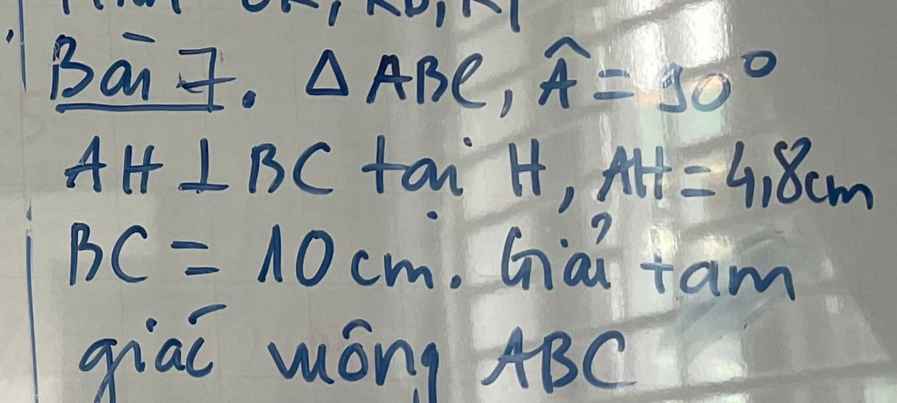



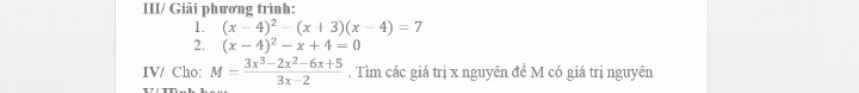
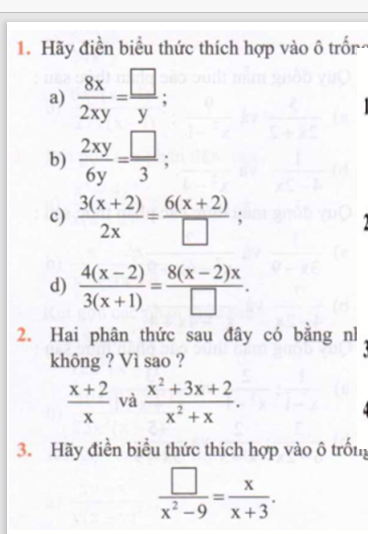 Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giải giúp em với ạ em đang cần gấp ạ Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giải giúp em với ạ em đang cần gấp ạ
a) \(\Leftrightarrow x^2+10x+25-x^2+8x-15=-8\\ \Leftrightarrow18x=-18\\ \Leftrightarrow x=-1\)
b) \(\Leftrightarrow\left(2x+1\right)^2-3\left(2x+1\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(2x+1-3\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(2x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)