Cho hình lăng trụ đều ABC.A'B'C' có góc giữa đường thẳng A'B với mặt phẳng (ABC) bằng
60
°
và khoảng cách từ điểm A đến mặt phẳng (A'BC) bằng
a
5
2
. Tính theo a thể tích V của khối lăng trụ ABC A'B'C'. A.
V
=
125
3
96
a
3
B.
V
=
125
3
288
a
3
C.
V
=
125
3
384
...
Đọc tiếp
Cho hình lăng trụ đều ABC.A'B'C' có góc giữa đường thẳng A'B với mặt phẳng (ABC) bằng 60 ° và khoảng cách từ điểm A đến mặt phẳng (A'BC) bằng a 5 2 . Tính theo a thể tích V của khối lăng trụ ABC A'B'C'.
A. V = 125 3 96 a 3
B. V = 125 3 288 a 3
C. V = 125 3 384 a 3
D. V = 125 3 48 a 3
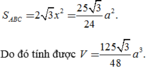
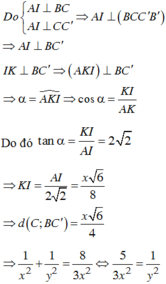
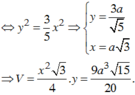
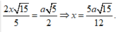
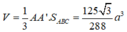
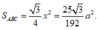
Đáp án A
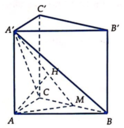
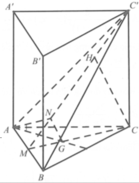
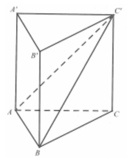
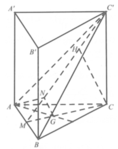
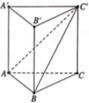
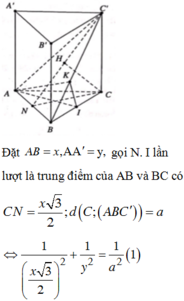
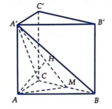
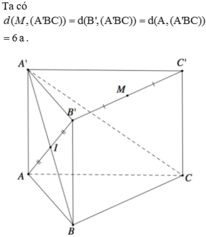
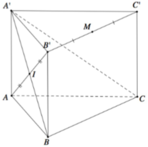
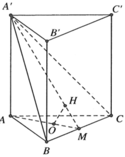
Gọi M là trung điểm của BC thì B C ⊥ A ' A M .
Từ A kẻ A H ⊥ A ' M , H ∈ A ' M . Khi đó A H ⊥ ( A ' B C ) .
Suy ra d A , A ' B C = A H = a 5 2 .
Góc giữa đường thẳng A ' B và mặt phẳng (ABC) bằng góc A ' M A ⏞ .
Theo giả thiết ta có A ' M A ⏞ = 60 °
Đặt AB = 2x thì A M = x 3 ; A ' A = 2 x 3 .
Suy ra A H = A ' A . A M A ' A 2 + A M 2 = 2 x 15 5
Từ giả thiết ta có 2 x 15 5 = a 5 2 ⇒ x = 5 a 15 12 Do đó
A A ' = 5 a 2 ; S A B C = 25 a 2 3 48
Vậy thể tích khối lăng trụ ABC.A'B'C' là V = 125 3 96 a 3 .