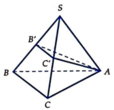
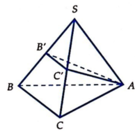
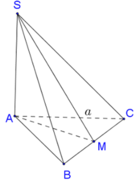
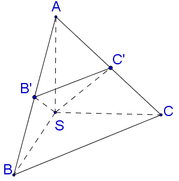
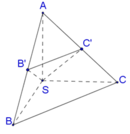
Cho hình chóp S.ABC có SA=SB=SC=a, A S B ⏞ = B S C ⏞ = C S A ⏞ = α . Gọi β là mặt phẳng đi qua A và các trung điểm của SB, SC. Tính diện tích thiết diện S của hình chóp cắt bởi mặt phẳng β .
A. S = a 2 2 7 cos 2 α - 16 cos α + 9
B. S = a 2 2 7 cos 2 α - 6 cos α + 9
C. S = a 2 8 7 cos 2 α - 6 cos α + 9
D. S = a 2 8 7 cos 2 α - 16 cos α + 9

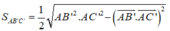
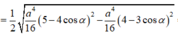
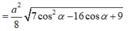

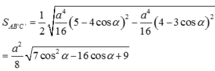
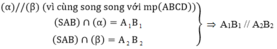

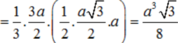


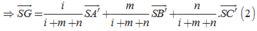

Đáp án D.
Gọi B',C' là trung điểm SB,SC ⇒ Thiết diện là Δ A B ' C '
Ta có S A ' B ' C ' = 1 2 A B ' 2 . A C ' 2 - A B ' → . A C ' → 2
A B ' → = 1 2 S B → - S A → ⇒ A B ' 2 = 1 4 S B 2 + S A 2 - S A → . S B → = a 2 4 5 - 4 cos α
Tương tự ta có A B ' → . A C ' → = a 2 4 4 - 3 cos α
Vậy S A B ' C ' = 1 2 a 4 16 5 - 4 cos α 2 - a 4 16 4 - 3 cos α 2 = a 2 8 7 cos 2 α - 16 cos α + 9