Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình dưới đây:
log (x - 40) + log (60 - x) < 2?
A. 20
B. 10
C. Vô số
D. 18
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 11 2017
Đáp án D
Điều kiện 40 < x < 60
P T ⇔ log x - 40 60 - x < 2 ⇔ x - 40 60 - x < 100 ⇔ x 2 - 100 x + 2500 > 0 ⇔ x - 50 2 > 0 ⇔ x ≠ 50 .
Vậy x cần tìm theo yêu cầu đề là các số nguyên dương chạy từ 41 đến 59; trừ giá trị 50. Có tất cả 18 giá trị thỏa mãn.
CM
21 tháng 1 2017
Đáp án B
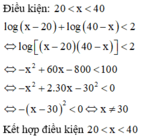
và x nguyên dương, vậy có 18 giá trị của x thỏa mãn đề bài.
CM
12 tháng 8 2018
Ta có:
8 x . 2 1 - x 2 > 2 2 x ⇔ 2 3 x + 1 - x 2 > 2 x ⇔ 3 x + 1 - x 2 > x ⇔ x 2 - 2 x - 1 < 0 ⇔ 1 - 2 < x < 1 + 2
Mà x ∈ ℝ ⇒ x ∈ 1 ; 2 . Bất phương trình đã cho có 2 nghiệm nguyên dương.
Chọn đáp án C.
Đáp án D
Điều kiện 40 < x < 60
Vậy x cần tìm theo yêu cầu đề là các số nguyên dương chạy từ 41 đến 59; trừ giá trị 50. Có tất cả 18 giá trị thỏa mãn.