Bộ số thực (x;y) thỏa mãn đẳng thức (3+x) + (1+y)i = 1+3i là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
15 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2022
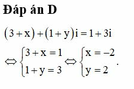
Nếu đề là \(f\left(x\right)=\sqrt{x^2+2x+1}\) và \(g\left(x\right)=4x^2-5x^2+1\left(???\right)\) thì cả \(f\left(x\right)\) và \(g\left(x\right)\) đều liên tục trên R
DG
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 9 2020
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge2009\\y\ge2010\end{matrix}\right.\)
\(\Leftrightarrow x-2009-2\sqrt{x-2009}+1+y-2010-2\sqrt{y-2010}+1=0\)
\(\Leftrightarrow\left(\sqrt{x-2009}-1\right)^2+\left(\sqrt{y-2010}-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-2009}-1=0\\\sqrt{y-2010}-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2010\\y=2011\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 1 2022
Đặt \(\left(\sqrt{x};2\sqrt{y};3\sqrt{z}\right)=\left(a;b;c\right)\Rightarrow a;b;c\ge0\)
Ta có:
\(\dfrac{2}{a+b+c}-\dfrac{1}{ab+bc+ca}\le\dfrac{2}{a+b+c}-\dfrac{3}{\left(a+b+c\right)^2}=-3\left(\dfrac{1}{a+b+c}-\dfrac{1}{3}\right)^2+\dfrac{1}{3}\le\dfrac{1}{3}\)
Đẳng thức xảy ra khi và chỉ khi: \(a=b=c=1\Rightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{1}{4}\\z=\dfrac{1}{9}\end{matrix}\right.\)
11 tháng 2 2017
\(\left(1\right)\Leftrightarrow z=x-y+1\)
Thế vào (2)\(xy+\left(x^2+y^2-2xy+2x-2y+1\right)-7\left(x-y+1\right)+10=0\)
\(x^2+y^2-xy-5x+5y+4\Leftrightarrow-xy-5\left(x-y\right)+21=0\left(3\right)\\ \)
\(\left(x-y\right)^2=17-2xy\Rightarrow-xy=\frac{\left(x-y\right)^2-17}{2}\) (4)đặt (x-y)=t
\(\left(3\right)\Leftrightarrow\frac{t^2-17}{2}-5t+21=0\Leftrightarrow t^2-10t+25\Rightarrow t=5\)
(1)=> z=6
(4) => xy=-4 hệ \(\left\{\begin{matrix}x-y=5\\xy=-4\end{matrix}\right.\)=> (y+5)y=y^2+5y+4=0=>\(\left\{\begin{matrix}y=-1\\y=-4\end{matrix}\right.\) \(\Rightarrow\left\{\begin{matrix}x=4\\x=1\end{matrix}\right.\)
Kết luận:
(x,y,z)=(1,-4,6);(4,-1,6)
H
10 tháng 6 2018
\(\sqrt{x-29}+2\sqrt{y-6}+3\sqrt{z-2011}+1016=\dfrac{1}{2}\left(x+y+z\right)\)\(\Leftrightarrow2\sqrt{x-29}+4\sqrt{y-6}+6\sqrt{z-2011}+2032=x+y+z\)\(\Leftrightarrow-2\sqrt{x-29}-4\sqrt{y-6}-6\sqrt{z-2011}-2032=-x-y-z\)\(\Leftrightarrow(x-29-2\sqrt{x-29}+1)+(y-6-2\cdot2\sqrt{y-6}+2^2)+(z-2011-2\cdot3\sqrt{z-2011}+3^2)=0\)\(\Leftrightarrow\left(\sqrt{x-29}-1\right)^2+\left(\sqrt{y-6}-2\right)^2+\left(\sqrt{z-2011}-3\right)^2=0\)\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-29}-1=0\\\sqrt{y-6}-2=0\\\sqrt{z-2011}-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-29}=1\\\sqrt{y-6}=2\\\sqrt{z-2011}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-29=1\\y-6=4\\z-2011=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=10\\z=2020\end{matrix}\right.\)
Vậy : ......................
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 5 2019
ĐKXĐ: ....
\(\Leftrightarrow2\sqrt{x-29}+4\sqrt{y-6}+6\sqrt{z-2011}+2032=x+y+z\)
\(\Leftrightarrow x-29-2\sqrt{x-29}+1+y-6-4\sqrt{y-6}+4+z-2011-6\sqrt{z-2011}+9=0\)
\(\Leftrightarrow\left(\sqrt{x-29}-1\right)^2+\left(\sqrt{y-6}-2\right)^2+\left(\sqrt{z-2011}-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-29}-1=0\\\sqrt{y-6}-2=0\\\sqrt{z-2011}-3=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=30\\y=10\\z=2020\end{matrix}\right.\)
