Một vật nhỏ dao động điêu hoà trên trục Ox với phương trình x = 4cos(ωt + 2π/3) cm. Trong giây đầu tiên kể từ t = 0, vật đi được quãng đường 4 cm. Trong giây thứ 2018 vật đi được quãng đường là
A. 3 cm.
B. 4 cm.
C. 2 cm.
D. 6 cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Biểu diễn dao động của vật tương ứng trên đường tròn.
+ Tại t = 0 , vật đi qua vị trí x = -0,5A = -2 cm theo chiều dương.
→ Sau khoảng thời gian 1 s, vật đi được quãng đường S = 0,5A+A = 6 cm → Vật đến biên.
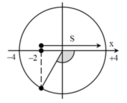
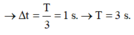
Ta chú ý rằng, sau khoảng thời gian 2016 s = 672 T vật quay về vị trí ban đầu → trong 1 s thứ 2017 vật cũng sẽ đi được quãng đường 6 cm.
Đáp án A

Đáp án D
Kể từ thời điểm gia tốc đạt độ lớn cực tiểu lần đầu tiên đến khi vectơ vận tốc đổi chiều lần đầu tiên, quãng đường vật đi được là A = 4 cm.

\(20-10\sqrt{2\left(A-\frac{A}{\sqrt{2}}\right)}\Rightarrow\frac{T}{4}=1\Rightarrow T=4\left(s\right)\)
\(S=S_{2012}-S_{2011}=A\sqrt{2}=10\sqrt{2}\) (cm)
Không có đáp án đó nhưng bạn giải thích cách làm của bạn cho mình với.

Chọn A
+ a =0 chính là vị trí đổi dấu; đổi chiều của gia tốc.
+ Biểu diễn trên đường tròn lượng giác, ta có: S = A/2 + A +A = 10cm.

Đáp án A
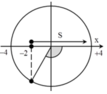
+ Biểu diễn dao động của vật tương ứng trên đường tròn
+Tại t=0,vật đi qua vị trí x=-0,5 A=-2cm theo chiều dương
->Sau khoảng thời gian 1 s, vật đi được quãng đường S = 0 , 5 A + A = 6 c m
Vật đến biên → Δ t = T 3 = 1 s . → T = 3 s .
+ Ta chú ý rằng, sau khoảng thời gian 2016 s = 672 T vật quay về vị trí ban đầu -> trong 1 s thứ 2017 vật cũng sẽ đi được quãng đường 6 cm

Đáp án A

+ Biểu diễn dao động của vật tương ứng trên đường tròn.
+ Tại t=0, vật đi qua vị trí x=-0,5 A=-2cm theo chiều dương
-> Sau khoảng thời gian 1 s, vật đi được quãng đường S=0,5A+A=6cm->Vật đến biên
→ Δ t = T 3 = 1 s . → T = 3 s .
+ Ta chú ý rằng, sau khoảng thời gian 2016 s = 672 T vật quay về vị trí ban đầu -> trong 1 s thứ 2017 vật cũng sẽ đi được quãng đường 6 cm
Chọn D.