Question

[Pham Trong Bach]

Thầy Tâm cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng 500 3 m 3 . Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500.000 đồng/ m 2 . Khi đó, kích thước của hồ nước như thể nào để chi phí thuê nhân công mà thầy Tâm phải trả thấp nhất:

A. Chiều dài 20m, chiều rộng 15m và chiều cao 20 3 m

B. Chiều dài 20m, chiều rộng 10m và chiều cao 5 6 m  

C. Chiều dài 10m, chiều rộng 5m và chiều cao 10 3 m  

D. Chiều dài 30m, chiều rộng 15m và chiều cao 10 27 m

Answer 1

[Cao Minh Tâm]

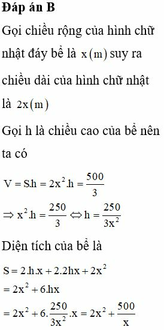
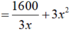
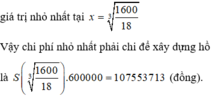
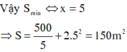
Đáp án là C.

 Gọi x là chiều rộng của đáy hình chữ nhật và y là chiều cao của khối hộp chữ nhật.

Để tốn ít nguyên vật liệu nhất, ta cần thiết kế sao cho diện tích toàn phần của khối hộp là lớn nhất.

Ta có: S x q = 2 x 2 + 2 x y + 2 2 x y = 2 x 2 + 6 x y  

Do V = 2 x 2 y ⇒ y = V 2 x 2

⇒ S x = 2 x 2 + 6 x V 2 x 2 = 2 x 2 + 3 V x

Do S, x phải luôn dương nên ta tìm giá trị nhỏ nhất của S trên 0 ; + ∞ .

Ta có:  S ' x = 4 x − 3 V x 2 , S ' x = 0 ⇔ x = 3 V 4 3

Lại có S ' ' x = 4 + 6 x 3 > 0 , ∀ x ∈ 0 ; + ∞ .

Do đó  min S = S 3 V 4 3 = 3 9 V 2 2 3

Và khi đó chiều cao là: y = V 2 x 2 = V 2 9 V 2 16 3 = 2 16 V 9 3  

Vậy: yêu cầu bài toán tương đương với chiều rộng đáy hình hộp là 5m, chiều dài là 10 m, chiều cao hình hộp là 10 3 m.