Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Chi phí thấp nhất khi diện tích xây dựng là thấp nhất. Gọi độ dài hai kích thước đáy là a,2a độ dài cạnh bên là B thì diện tích xây dựng là
M
Vậy chi phí thấp nhất là: 150.0.5=75 trệu đồng

Đáp án B
Giá thuê công nhân nhỏ nhất khi chiếc bể có diện tích nhỏ nhất.


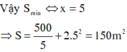
=> Tiền công = 150.500000 = 75 triệu đồng

Đáp án C
Giả sử các kích thước đáy là x và 2 x . Chiều cao bể nước là y.
Ta có V = 2 x 2 y = 500 3
Để chi phí thuê công nhân ít nhất thì diện tích xây là nhỏ nhẩt
Ta có
S x = S x q + S d = 6 x y + 2 x 2 = 6 x . 500 3.2 x 2 + 2 x 2 = 500 x + 2 x 2
= 250 x + 250 x + 2 x 2 ≥ 3 250 x + 250 x + 2 x 2 3 = 150 m 2 ⇒ T min = 15 triệu đồng

Đáp án B
Gọi chiều cao của đáy là 2x và chiều rộng là x. Chiều cao của hồ là h
Khi đó V = 2 x 2 h = 500 3 ⇒ h = 500 6 x 2
Phần diện tích cần xây (bao gồm đáy hộ và phần abo quanh) là
S = 2 x 2 + 6 x h = 2 x 2 + 6 x . 500 6 x 2 = 2 x 2 + 500 x = 2 x 2 + 250 x + 250 x ≥ 2 x 2 . 250 x . 250 x 3 = 150
(Bất đẳng thức AM-GM). Dấu bằng xảy ra ⇔ 2 x 2 = 250 x ⇒ x = 5 m
Khi đó chi phí là 600000.150=90.000.000
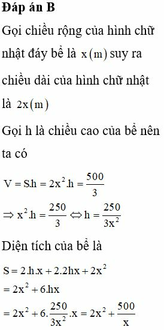



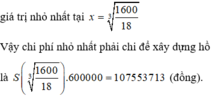




Đáp án là C.
Gọi x là chiều rộng của đáy hình chữ nhật và y là chiều cao của khối hộp chữ nhật.
Để tốn ít nguyên vật liệu nhất, ta cần thiết kế sao cho diện tích toàn phần của khối hộp là lớn nhất.
Ta có: S x q = 2 x 2 + 2 x y + 2 2 x y = 2 x 2 + 6 x y
Do V = 2 x 2 y ⇒ y = V 2 x 2
⇒ S x = 2 x 2 + 6 x V 2 x 2 = 2 x 2 + 3 V x
Do S, x phải luôn dương nên ta tìm giá trị nhỏ nhất của S trên 0 ; + ∞ .
Ta có: S ' x = 4 x − 3 V x 2 , S ' x = 0 ⇔ x = 3 V 4 3
Lại có S ' ' x = 4 + 6 x 3 > 0 , ∀ x ∈ 0 ; + ∞ .
Do đó min S = S 3 V 4 3 = 3 9 V 2 2 3
Và khi đó chiều cao là: y = V 2 x 2 = V 2 9 V 2 16 3 = 2 16 V 9 3
Vậy: yêu cầu bài toán tương đương với chiều rộng đáy hình hộp là 5m, chiều dài là 10 m, chiều cao hình hộp là 10 3 m.