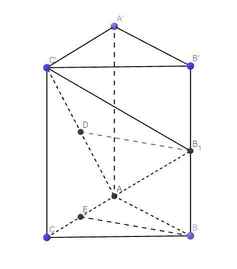
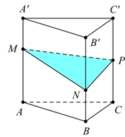
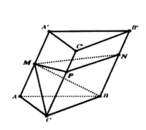
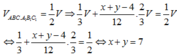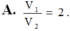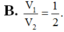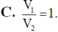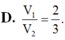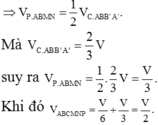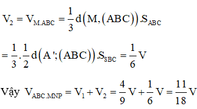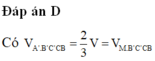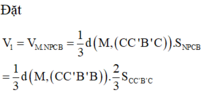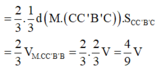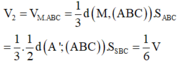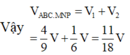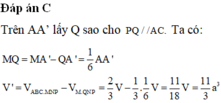Cho hình lăng trụ tam giác ABC.A’B’C’ có thể tích là V và độ dài cạnh bên là AA’=6 đơn vị. Cho điểm A1 thuộc cạnh AA’ sao cho AA1=2. Các điểm B1, C1 lần lượt thuộc cạnh BB’, CC’ sao cho BB1=x, CC1=y. Biết rằng thể tích khối đa diện ABC. A1B1C1 bằng 1/2V. Giá trị của x+y bằng
A. 10
B. 4
C. 16
D. 7