Cho tứ diện ABCD. Hai điểm M, N lần lượt di động trên 2 đoạn thẳng BC và BD sao cho 2 B C B M + 3 B D B N = 10 . Gọi V 1 , V 2 lần lượt là thể tích của các khối tứ diện ABMN và ABCD. Tìm giá trị nhỏ nhất của V 1 V 2
A. 3 8
B. 5 8
C. 2 7
D. 6 25
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

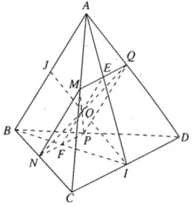
a) 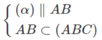
⇒ (α) ∩ (ABC) = MN và MN // AB
Ta có N ∈ (BCD) và 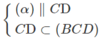
Nên ⇒ (α) ∩ (BCD) = NP và NP // CD
Ta có P ∈ (ABD)
Và 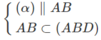 nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
 nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
Do đó MN // PQ và NP // MQ, Vậy tứ giác MNPQ là hình bình hành.
b) Ta có: MP ∩ NQ = O. Gọi I là trung điểm của CD.
Trong tam giác ACD có : MQ // CD ⇒ AI cắt MQ tại trung điểm E của MQ.
Trong tam giác ACD có : NP // CD ⇒ BI cắt NP tại trung điểm F của NP.
Vì MNPQ là hình bình hành nên ta có
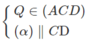
EF // MN ⇒ EF // AB
Trong ΔABI ta có EF // AB suy ra : IO cắt AB tại trung điểm J
⇒ I, O, J thẳng hàng
⇒ O ∈ IJ cố định.
Vì M di động trên đoạn AC nên Ochạy trong đoạn IJ .
Vậy tập hợp các điểm O là đoạn IJ.

cho hình vuông ABCD, I là 1 điểm thuộc CD. Gọi O là gia điểm AC và BD. Qua I kẻ đường thẳng song song với AC, cắt BD và AD lần lượt ở E và M. Qua I kẻ đường thẳng vuông góc AC tại K và Cắt BC tại N.
a, Tứ giác EOKI là hình gì? Vì sao?
b, C/m : M, O,N thẳng hàng
c,C/m : Khi I di động trên CD thì chu vi tứ giác EOKI không đổi?

Chọn mặt phẳng phụ chứa CD là (BCD)
Do NP không song song CD nên NP cắt CD tại E
Điểm E ∈ N P ⇒ E ∈ M N P .
Vậy C D ∩ M N P tại E.
Chọn A

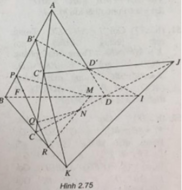
a) Chú ý rằng I, J, K thẳng hàng vì chúng cùng thuộc giao tuyến của hai mặt phẳng (CBD) và (C'B'D')
b) 4. Vì 4 điểm không đồng phẳng sẽ tạo nên 1 tứ diện => có 4 mặt
Đáp án D