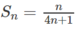OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

Mini game 20/11 tri ân thầy cô, nhận thưởng hấp dẫn - Tham gia ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
20 tháng 8 2018
Cho tổng:  S n   =   1 1 . 5   +   1 5 . 9   +   . . .   +   1 4 n - 3 4 n + 1 a) Tính S 1 ,   S 2 ,   S 3 ,   S 4 ; b) Dự đoán công thức tính S n  và chứng minh bằng phương pháp quy...
Đọc tiếp

Cho tổng:  S n   =   1 1 . 5   +   1 5 . 9   +   . . .   +   1 4 n - 3 4 n + 1

a) Tính S 1 ,   S 2 ,   S 3 ,   S 4 ;

 

b) Dự đoán công thức tính S n  và chứng minh bằng phương pháp quy nạp.
#Toán lớp 11
1
CM
Cao Minh Tâm
20 tháng 8 2018

a) Tính

Giải sách bài tập Toán 11 | Giải sbt Toán 11

b) Viết lại

Giải sách bài tập Toán 11 | Giải sbt Toán 11

Ta có thể dự đoán Giải sách bài tập Toán 11 | Giải sbt Toán 11

Đúng(0)
NP
NGUYỄN PHƯỚC NHÂN
12 tháng 2 2019
Tính toán 1) S = 1+2+3+4+...+n 2) S = 1*2*3...*n 3)S = 2+4+6+...+n 4)S = 1+3+5+...+n 5)S = 2*4*6...*n 6)S = 1-2+3-4+...+n 7)S = -1+2-3+4+...+n 8)S = 1+4+9+16+...+n*n 9)S = 1+9+25+...+( n mod 2 = 1)^2 10)S =4+16+...+( n mod 2 = 0)^2 11)S =5+10+15+...+ n mod 5 =0 12)S = 1+2-3+4+5-6+7+8-9...+n-(n mod 3 = 0 ) 13)S = 1+2!+3!+4!...+n! 14)S =1+(1+2)+(1+2+3)+...+( tổng các số từ 1 tới )( i chạy từ 1 tới n) 15)S =1*2+2*3+4*5+...+(n-1)*n HELP...
Đọc tiếp

Tính toán

1) S = 1+2+3+4+...+n

2) S = 1*2*3...*n

3)S = 2+4+6+...+n

4)S = 1+3+5+...+n

5)S = 2*4*6...*n

6)S = 1-2+3-4+...+n

7)S = -1+2-3+4+...+n

8)S = 1+4+9+16+...+n*n

9)S = 1+9+25+...+( n mod 2 = 1)^2

10)S =4+16+...+( n mod 2 = 0)^2

11)S =5+10+15+...+ n mod 5 =0

12)S = 1+2-3+4+5-6+7+8-9...+n-(n mod 3 = 0 )

13)S = 1+2!+3!+4!...+n!

14)S =1+(1+2)+(1+2+3)+...+( tổng các số từ 1 tới )( i chạy từ 1 tới n)

15)S =1*2+2*3+4*5+...+(n-1)*n

HELP ME!
#Tin học lớp 8
0
TT
thu thu
17 tháng 4 2023

cho tổng s= 1-2-3+4+5-6-7+8+9 -10-11 +12... n. viết chương trình nhập vào một số n tính tổng từ 1 đến n pascal
#Tin học lớp 11
0
PK
Phan Khánh Quỳnh
24 tháng 5 2019
1, tính tổng : viết chương trình cho phép nhập số nguyên dương n từ bàn phím yêu cầu tính và in ra màn hình tổng s= 1+3+5+7+.......2*n+1 dữ liệu vào dữ liệu ra giải thích n=1 s=4 s=1+3=4 n=2 s=9 s=1+3+5=9 nhanh , tui cần...
Đọc tiếp

1, tính tổng : viết chương trình cho phép nhập số nguyên dương n từ bàn phím yêu cầu

tính và in ra màn hình tổng s= 1+3+5+7+.......2*n+1

dữ liệu vào dữ liệu ra giải thích
n=1 s=4 s=1+3=4
n=2 s=9

s=1+3+5=9

nhanh , tui cần gấp
#Tin học lớp 8
1
NT
Nguyễn Trung Hiếu
24 tháng 5 2019

uses crt;
var n,n1,s:real;
begin
clrscr;
write('Nhap n: ');readln(n);
n1:=2*n+1;
s:=((n1 - 1)/2+1)*(n1 + 1)/2;
write(s:0:0);
readln
end.

Đúng(0)
NT
Nguyễn Thị Ngọc Hà
25 tháng 3 2017

Bài 1: tính giá trị biểu thức:

A=5/12+3/4-1 trên 3-5/6+2/3 + 16/5+16/7-16/9 trên 17/5+17/7-17/9

Bài 2: So sánh tổng:

S=1/5+1/9+1/10+1/41+1/42 với 1/2

BN NÀO HOK GIỎI TOÁN GIÚP MK VỚI ! Cảm ơn!
#Toán lớp 6
4
BN
Bùi Ngọc Minh
25 tháng 3 2017

Bài 1:

A=\(\dfrac{\dfrac{5}{12}+\dfrac{3}{4}-1}{3-\dfrac{5}{6}+\dfrac{2}{3}}+\dfrac{\dfrac{16}{5}+\dfrac{16}{7}-\dfrac{16}{9}}{\dfrac{17}{5}+\dfrac{17}{7}-\dfrac{17}{9}}\)

A=\(\dfrac{\dfrac{1}{6}}{\dfrac{17}{6}}+\dfrac{16\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}\right)}{17\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}\right)}\)

A=\(\dfrac{1.\dfrac{1}{6}}{17.\dfrac{1}{6}}+\dfrac{16}{17}\)

A=\(\dfrac{1}{17}+\dfrac{16}{17}=\dfrac{17}{17}=1\)

Bài 2 mk chưa có câu trả lời, sorry nha!

Đúng(0)
PT
Phạm Thị Hiền Mai
25 tháng 3 2017

bn ghép cac so lai voi nhau nhe

Đúng(0)
NT
Nguyễn Thái Bảo
22 tháng 7 2023 - olm

bai 1 :tính tổng  N=1^2+2^2+3^2+...+99^2

bài2: tính tổng A=1+4+9+16+25+36+...+100000

bài3: tính tổng S=1^2+3^2+5^2+...+49^2

bài4:tính tổng S=1^2+3^2+5^2+...+99^2

giúp mik với mik đang cần gấp
#Toán lớp 6
3
NN
Nguyễn Ngọc Anh Minh
CTVHS VIP
22 tháng 7 2023

1/

\(N=1.\left(2-1\right)+2\left(3-1\right)+3\left(4-1\right)+...+99\left(100-1\right)=\)

\(=\left(1.2+2.3+3.4+...+99.100\right)-\left(1+2+3+...+99\right)=\)

Đặt 

\(A=1.2+2.3+3.4+...+99.100\)

\(3A=1.2.3+2.3.3+3.4.3+...+99.100.3=\)

\(=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+99.100.\left(101-98\right)=\)

\(=1.2.3-1.2.3+2.3.4-2.3.4+3.4.5-...-98.99.100+99.100.101=\)

\(=99.100.101\Rightarrow A=\dfrac{99.100.101}{3}=33.100.101\)

Đặt

\(B=1+2+3+...+99=\dfrac{99.\left(1+99\right)}{2}=4950\)

\(\Rightarrow N=A-B\)

2/

Số hạng cuối cùng là 10000 hoặc 1000000 mới làm được

\(A=1^2+2^2+3^2+...+100^2\) 

Tính như câu 1

3/ Làm như bài 4

4/

\(S=1^2+3^2+5^2+...+99^2=\)

\(=1.\left(3-2\right)+3\left(5-2\right)+5\left(7-2\right)+...+99\left(101-2\right)=\)

\(=\left(1.3+3.5+5.7+...+99.101\right)-2\left(1+3+5+...+99\right)\)

Đặt

\(B=1+3+5+...+99=\dfrac{50.\left(1+99\right)}{2}=2500\) 

Đặt

\(A=1.3+3.5+5.7+...+99.101\)

\(6A=1.3.6+3.5.6+3.7.6+...+99.101.6=\)

\(=1.3.\left(5+1\right)+3.5.\left(7-1\right)+5.7.\left(9-3\right)+...+99.101.\left(103-97\right)=\)

\(=1.3+1.3.5-1.3.5+3.5.7-3.5.7+5.7.9-...-97.99.101+99.101.103=\)

\(=3+99.101.103\Rightarrow A=\dfrac{3+99.101.103}{6}\)

\(\Rightarrow S=A-2B\)

Đúng(2)
GH
Gia Hân
VIP
22 tháng 7 2023

Bài 1:

\(N=1^2+2^2+3^3+...+99^2\)

\(N=1.1+2.2+3.3+...+99.99\)

\(N=1.\left(2-1\right)+2.\left(3-1\right)+3.\left(4-1\right)+...+99.\left(100-1\right)\)

\(N=1.2-1+2.3-2+3.4-3+...+99.100-99\)

\(N=\left(1.2+2.3+3.4+...+99.100\right)-\left(1+2+3+...+99\right)\)

Đặt \(\left\{{}\begin{matrix}A=1.2+2.3+3.4+...+99.100\\B=1+2+3+...+99\end{matrix}\right.\)

+) Tính \(A=1.2+2.3+3.4+...+99.100\)

Ta có:

\(3A=1.2.3+2.3.3+3.4.3+...+99.100.3\)

\(3A=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+99.100.\left(101-98\right)\)

\(3A=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+99.100.101-98.99.100\)

\(3A=99.100.101\)

\(\Rightarrow A=\dfrac{99.100.101}{3}=333300\)

+) Tính \(B=1+2+3+...+99\)

\(B\) có số số hạng là: \(\dfrac{99-1}{1}\) + 1 = 99 (số hạng)

\(\Rightarrow B=\dfrac{\left(99+1\right).99}{2}=4950\)

\(\Rightarrow N=A-B=333300-4950=328350\)

\(\Rightarrow N=328350\)

 

 

Đúng(0)
EA
Erika Alexandra
25 tháng 2 2017
Bài 1: cho A = 999......9 (n chữ số 9). So sánh tổng các chữ số của A và tổng các chữ số của A^2. Bài 2: Tìm n thuộc Z để n^2+9n+7 chia hết cho n+2. Baig 3: Tìm các ước chung của 12n+1 và 30n+2. Bài 4: So sánh A và 1/4 biết: A= 1/2^3 + 1/3^3 + 1/4^3 + ... + 1/n^3. Bài 5: So sánh 1/40 và B=1/5^3 + 1/6^3 + ... + 1/2004^3. Bài 6: Tìm x, y biết: x/2 = y/5 và 2x-y=3 Bài 7: Tìm x, y biết: x/2=y/5 và x . y =...
Đọc tiếp

Bài 1: cho A = 999......9 (n chữ số 9). So sánh tổng các chữ số của A và tổng các chữ số của A^2.

Bài 2: Tìm n thuộc Z để n^2+9n+7 chia hết cho n+2.

Baig 3: Tìm các ước chung của 12n+1 và 30n+2.

Bài 4: So sánh A và 1/4 biết:

A= 1/2^3 + 1/3^3 + 1/4^3 + ... + 1/n^3.

Bài 5: So sánh 1/40 và B=1/5^3 + 1/6^3 + ... + 1/2004^3.

Bài 6: Tìm x, y biết:

x/2 = y/5 và 2x-y=3

Bài 7: Tìm x, y biết:

x/2=y/5 và x . y = 10
#Toán lớp 6
1
MV
Mới vô
10 tháng 6 2017

Bài 1:

Tổng các chữ số của \(A\) là \(9n\)

\(A^2=99...9800...01\left(n-1\text{ chữ số }9\text{ và chữ số }0\right)\)

Vậy tổng các chữ số của \(A^2\) là \(\left(9+0\right)\left(n-1\right)+8+1=9\left(n-1\right)+9=9\left(n-1+1\right)=9n\)

Vậy tổng các chữ số của \(A\) bằng tổng các chữ số của \(A^2\) .

Đúng(0)
HN
Huy Nguyễn
2 tháng 3 2016 - olm

Cho S= 1/n+3 + 1/n+4 + 1/n+5 +...+ 1/n+2015 vơis n là số tự nhiên Chứng minh rằng với mọi giá trị của n tổng S không phải số tự nhiên
#Toán lớp 6
0
NA
Nhật Anh
23 tháng 12 2021
 Câu 30. Cho thuật toán tính tổng s= -1+2-3+4+…+n(-1)n sử dụng phương pháp liệt kê dưới đây:Bước 1: Nhập NBước 2: i ← 0, s← 1;Bước 3: i ← i+1Bước 4: Nếu i > N thì đưa ra tổng s và kết thúc chương trình.Bước 5: Nếu i chia hết cho 2 thì s ← s+i, quay lại B3Bước 6: Nếu i không chia hết cho 2 thì s ← s-i, quay lại B3Hãy cho biết bước sai trong thuật toán trên:A. Bước 2B. Bước 3C. Bước 4D. Bước 5  Câu 31: . Cho dãy a = 2  ...
Đọc tiếp

 

Câu 30. Cho thuật toán tính tổng s= -1+2-3+4+…+n(-1)n sử dụng phương pháp liệt kê dưới đây:

Bước 1: Nhập N

Bước 2: i ← 0, s← 1;

Bước 3: i ← i+1

Bước 4: Nếu i > N thì đưa ra tổng s và kết thúc chương trình.

Bước 5: Nếu i chia hết cho 2 thì s ← s+i, quay lại B3

Bước 6: Nếu i không chia hết cho 2 thì s ← s-i, quay lại B3

Hãy cho biết bước sai trong thuật toán trên:

A. Bước 2

B. Bước 3

C. Bước 4

D. Bước 5

 

 

Câu 31: . Cho dãy a = 2   4    7   6    8    9    5   12    13     3. 

Hỏi sau khi thực hiện xong thuật toán s = ?

B1: i ← 1 , s ← 0

B2: Nếu i > 10 thì đưa ra s rồi kết thúc

B3: s ← s + ai

B4:

    4.1: Nếu ai chia hết cho 2 thì i ← i + 1

    4.2: i ← i + 2

B5: Quay lại B2

A. 10

B. 20 

C. 16

D. Chương trình lỗi

 

 

Câu 32: Cho dãy a = 5   7   3   11   4    6   2   8. Cho biết giá trị x sau khi thực hiện xong thuật toán?

B1: i ← 1, x ← 0

B2: Nếu i > 8 thì đưa ra x rồi kết thúc

B3:

    3.1: Nếu i chia hết cho 2 thì  x ← x + ai. Trái lại x ← x - ai

    3.2: i ← i + 1 , quay lại B2

A. Tính hiệu a-b

B. Tính giá trị tuyệt đối của a-b

C. Tính hiệu b-a

D. Trả ra số 4,8

 

Câu 33: Cho n = 7; k = 4; a = 10     8      7      20       12      6      1. 

Hỏi sau khi thực hiện xong thuật toán T = ?

B1: Nhập k, n, và dãy  a1, a2, … an, 

B2: T ← 0 

B3: Nếu i > n đưa ra T rồi kết thúc

B4: Nếu ai  chia hết cho k thì T ← T + ai

B5: i ← i + 1, quay lại B3  

A. 1

B. 0

C. Không hiển thị gì    

Chọn đáp án và sửa lại chỗ sai  
#Tin học lớp 10
1
NL
Nguyễn Lê Phước Thịnh
24 tháng 12 2021

Câu 30: A

Đúng(0)
ML
Minh Lê
15 tháng 2 2022

viết chương trình tính tổng

 s= 1*2/3*4+2*3/4*5+3*4/5*6+...+n*(n+1)/(n+2)*(n+3)
#Tin học lớp 8
1
NL
Nguyễn Lê Phước Thịnh
15 tháng 2 2022

uses crt;

var s:real;

i,n:integer;

begin

clrscr;

readln(n);

s:=0;

for i:=1 to n do 

  s:=s+(n*(n+1))/((n+2)*(n+3));

writeln(s:4:2);

readln;

end.

Đúng(2)
HT
Hoài thịnh
19 tháng 4 2023

Mọi người giúp mình câu này với ạ : 

Tính tổng : S= 1-2-3+4+5-6-7+8+9-10-11+12+...+n

Viết chương trình pascal nhập vào một số n tính tổng từ 1 đến n theo 2 cách

 
#Tin học lớp 11
0
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP