người ta đẩy một cái thùng có khối lượng 40kg theo phương ngang với một lực là 240N làm thùng chuyển động trên mặt phẳng ngang . hệ số ma sát trượt giữa thùng và mặt phẳng là 0,25. tính gia tốc của thùng . lấy g = 9,8m/s2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 1 2023
Định luật ll Niu tơn: \(\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m.a\)
\(\Rightarrow F-\mu mg=m.a\)
Gia tốc thùng:
\(\Rightarrow a=\dfrac{F-\mu mg}{m}=\dfrac{180-0,25\cdot50\cdot9,8}{50}=1,15\left(m/s^2\right)\)
VT
2 tháng 9 2017
Chọn chiều của lực tác dụng làm chiều dương:
F m s = μ t mg = 0,35.55.9,8 = 188,65 N ≈ 189 N
Do đó a = (F - F m s )/m = (220 - 189)/55 ≈ 0,56(m/ s 2 )
TK
13 tháng 12 2021
Theo định luật II Niu tơn
\(\overrightarrow{F_k}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m\cdot\overrightarrow{a}\)
Chiếu lên Oy: \(N=P=mg\)
Chiếu lên Ox: \(F_k-F_{ms}=m\cdot a\Rightarrow a=\dfrac{F_k-\mu\cdot m\cdot g}{m}\)
\(a=\dfrac{200-0,3\cdot50\cdot10}{50}=1\left(\dfrac{m}{s^2}\right)\)
VT
8 tháng 9 2017
Lực ma sát tác dụng vào thùng là:
→ F m s = μ N = μ m g = 0 , 35.50.10 = 175 N
Nhận thấy Lực ma sát tác dụng vào thùng lớn hơn lực đẩy của người đẩy thùng nên thùng không chuyển động.
Đáp án: C
28 tháng 11 2021
Định luật ll Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m\cdot a\) (1)
Lực ma sát: \(F_{ms}=\mu mg=0,02\cdot80\cdot10=16N\)
Thay vào (1) ta đc:
\(\Rightarrow a=\dfrac{F-F_{ms}}{m}=\dfrac{150-16}{80}=1,675\)m/s2
Chọn B.
28 tháng 12 2023
Chọn chiều (+) là chiều chuyển động của vật.
Vật được kéo trên mặt phẳng nằm ngang \(\Rightarrow N=P=mg=15.10=150\left(N\right)\)
Lực ma sát \(F_{ms}=\mu N=0,05.150=7,5\left(N\right)\)
Áp dụng định luật II Newton, ta có \(\overrightarrow{F}=m\overrightarrow{a}\) (1)
Chiếu (1) lên phương chuyển động của vật, ta có:
\(F_k-F_{ms}=ma\Rightarrow a=\dfrac{F_k-F_{ms}}{m}=\dfrac{45-7,5}{15}=2,5\left(m/s^2\right)\)
Vậy gia tốc của thùng là \(2,5m/s^2\).
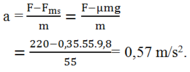
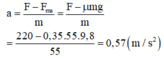
Theo định luật II Newton: \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
Chiếu phương trình lên Oy: \(N-P=0\Rightarrow N=P=mg=40.9,8=392\left(N\right)\)
Chiếu phương trình lên Ox: \(-F_{ms}+F=ma\)
\(\Rightarrow-\mu N+F=ma\)
\(\Rightarrow a=\dfrac{F-\mu N}{m}=\dfrac{240-0,25.392}{40}=3,55\left(\dfrac{m}{s^2}\right)\)
Chọn hệ trục Oxy như hình.
Chiều dương là chiều chuuyeern động.
Theo định luật ll Niu-tơn:
\(\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F}=m.\overrightarrow{a}\) (1)
Chiếu lên trục Ox ta đc:
\(F-F_{ms}=ma\) (2)
Chiếu (1) lên trục Oy ta đc:
\(N-P=0\Rightarrow N=P=mg\) (3)
\(F_{ms}=\mu\cdot N\) (4)
Từ \(\left(2\right).\left(3\right),\left(4\right)\) ta suy ra:
\(F-F_{ms}=ma\)
\(\Rightarrow a=\dfrac{F-F_{ms}}{m}=\dfrac{240-0,25\cdot40\cdot9,8}{40}=3,55\)m/s2