Xét tính chẵn lẻ của các hàm số sau: y = x2 + x + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 10 2021
TXĐ: D=R
Nếu \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=-2\cdot\left(-x\right)^4+\left(-x\right)^2-10\)
\(=-2x^4+x^2-10\)
=f(x)
=>f(x) là hàm số chẵn
PT
1
CM
8 tháng 2 2018
Tập xác định D = R\{0} nên nếu x ≠ 0 và x ∈ D thì -x ∈ D
Vậy hàm số đã cho là hàm số lẻ.
CM
5 tháng 12 2017
Đặt y = f(x) = |x|.
+ Tập xác định D = R nên với ∀ x ∈ D thì –x ∈ D.
+ f(–x) = |–x| = |x| = f(x).
Vậy hàm số y = |x| là hàm số chẵn.
CM
5 tháng 5 2017
Đặt y = f(x) = x3 + x.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)3 + (–x) = –x3 – x = – (x3 + x) = –f(x)
Vậy y = x3 + x là một hàm số lẻ.
CM
3 tháng 11 2018
Đặt y = f(x) = (x + 2)2.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x + 2)2 = (x – 2)2 ≠ (x + 2)2 = f(x)
+ f(–x) = (–x + 2)2 = (x – 2)2 ≠ – (x + 2)2 = –f(x).
Vậy hàm số y = (x + 2)2 không chẵn, không lẻ.
CM
17 tháng 2 2018
y = f(x) = 1/x
TXĐ: D = R \{0} ⇒ x ∈ D thì-x ∈ D
f(-x) = 1/(-x) = -1/x = -f(x)
Vậy y = f(x) = 1/x là hàm số lẻ.
TA
17 tháng 6 2021
Đặt `y=f(x)=x-sinx`
Có: `f(-x)=-x-sin(-x)=-x+sinx=-(x-sinx)=-f(x)`
`=>` Hàm lẻ.
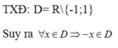
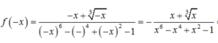
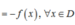
Đặt y = f(x) = x2 + x + 1.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ x2 + x + 1 = f(x)
+ f(–x) = (–x)2 + (–x) + 1 = x2 – x + 1 ≠ –(x2 + x + 1) = –f(x)
Vậy hàm số y = x2 + x + 1 không chẵn, không lẻ.