Cho hình lập phương (H). Gọi (H’) là hình bát diện đều có các đỉnh là tâm các mặt của (H). Tính tỉ số diện tích toàn phần của (H) và (H’).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 11 2017
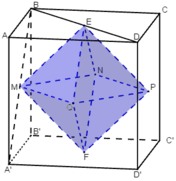
Gọi a là cạnh của hình lập phương ABCD.A1B1C1D1;
⇒ Diện tích toàn phần của hình lập phương (H) là: SH = 6.a2 (đvdt).
Gọi tâm các mặt lần lượt là E, F, M, N, P, Q như hình vẽ.
⇒ (H’) là bát diện đều EMNPQF.
+ Áp dụng định lí pytago vào tam giác vuông AA’D ⇒ A’D = a√2
+ EM là đường trung bình của ΔBA’D
QUẢNG CÁO
⇒ (H’) là bát diện đều gồm 8 mặt là các tam giác đều cạnh bằng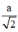 
⇒ Diện tích một mặt của (H’) là:
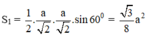
⇒ Diện tích toàn phần của (H’) là:
Vậy tỉ số diện tích cần tính là:
1 tháng 4 2017
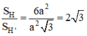
Cho hình lập phương ABCD.A’B’C’D’ . Gọi E, F, G, I, J, K là tâm của các mặt của nó. Khi đó các đỉnh E, F, G, I, J, K tạo thành hình bát diện đều EFGIJK.
Đặt AB = a, thì 
Diện tích tam giác đều (EFJ) bằng .gif)
.
Suy ra diện tích toàn phần của hình bát diện (H’) bằng .gif)
. Diện tích toàn phần của hình lập phương (H) bằng .gif)
. Do đó tỉ số diện tích toàn phần của (H) và (H') bằng
.gif)
.
CM
24 tháng 6 2019
Đáp án C.
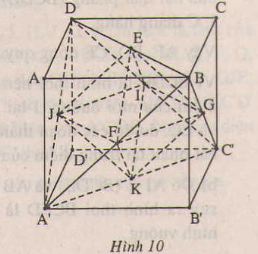
Cho hình lập phương ABCD.A'B'C'D'. Gọi E,F,G,I,J,K là tâm các mặt của nó. Khi đó các đỉnh E,F,G,I,J,K tạo thành hình bát diện đều EFGHIJK.
Đặt A B = a thì E J = A ' B 2 = a 2 2 .
Thể tích của khối bát diện đều có cạnh bằng x được tính bằng công thức V = x 3 2 3 . Áp dụng vào bài toán ta có V E F G Ị K = 1 3 . a 2 2 3 . 2 = a 3 6 .
Vậy tỉ số thể tích cần tìm là a 3 6 a 3 = 1 6 .
CM
29 tháng 1 2019
Đáp án C.
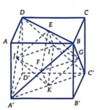
Đặt (H) là hình tứ diện đều ABCD, cạnh bằng A. Gọi E ; F ; I ; J lần lượt là tâm của các mặt A B C ; A B D ; A C D ; B C D .
Kí hiệu như hình vẽ.
Ta có M E M C = M F M D = 1 3 ⇒ E F C D = 1 3 ⇒ E F = C D 3 = a 3 .
Vậy tứ diện là tứ diện đều có cạnh bằng a 3 .
Tỉ số thể tích của diện tích toàn phần tứ diện đều và tứ diện đều ABCD là a 3 a 2 = 1 9
CM
6 tháng 7 2017
Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là a/2. Khi đó
Từ đó suy ra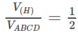 
20 tháng 5 2017
Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là \(\dfrac{a}{2}\). Khi đó :
\(V_{ABCD}=a^3\dfrac{\sqrt{2}}{12};V_{\left(H\right)}=\dfrac{1}{3}\left(\dfrac{a}{2}\right)^3\sqrt{2}=a^3\dfrac{\sqrt{2}}{24}\)
Từ đó suy ra :
\(\dfrac{V_{\left(H\right)}}{V_{ }ABCD}=\dfrac{1}{2}\)
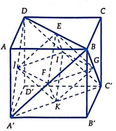
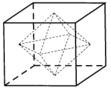
Gọi a là cạnh của hình lập phương ABCD. A 1 B 1 C 1 D 1 ;
⇒ Diện tích toàn phần của hình lập phương (H) là: SH = 6.a2 (đvdt).
Gọi tâm các mặt lần lượt là E, F, M, N, P, Q như hình vẽ.
⇒ (H’) là bát diện đều EMNPQF.
+ Áp dụng định lí pytago vào tam giác vuông AA’D ⇒ A’D = a√2
+ EM là đường trung bình của ΔBA’D
⇒ (H’) là bát diện đều gồm 8 mặt là các tam giác đều cạnh bằng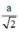
⇒ Diện tích một mặt của (H’) là:
⇒ Diện tích toàn phần của (H’) là:
Vậy tỉ số diện tích cần tính là: