Chứng minh rằng phương trình cos2x = sinx − 2 có ít nhất hai nghiệm trong khoảng - π 6 ; π
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
y' = -2cosxsinx + cosx = cosx(1 – 2sinx)
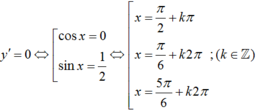
Vì 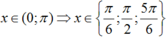 . Vậy có 3 nghiệm thuộc khoảng (0; π).
. Vậy có 3 nghiệm thuộc khoảng (0; π).

Chọn A
Ta có sin3x+ cos2x- sinx= 0 ⇔ cos2x(2sinx+1)=0. Lưu ý trong khoảng (0;π), sinx > 0

Đặt f(x) = x5 – 3x4 + 5x – 2
f(x) là hàm đa thức nên liên tục trên R.
Ta có: f(0) = –2 < 0
f(1) = 1 > 0
f(2) = -8 < 0
f(3) = 13 > 0
⇒ f(0).f(1) < 0; f(1).f(2) < 0; f(2).f(3) < 0
⇒ Phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc khoảng (0; 1); 1 nghiệm thuộc khoảng (1; 2); 1 nghiệm thuộc khoảng (2; 3)
⇒ f(x) = 0 có ít nhất 3 nghiệm thuộc (0; 3) hay f(x) = 0 có ít nhất 3 nghiệm thuộc (-2; 5).

\(\Leftrightarrow\left(1-sinx\right)\left(cos2x+3msinx+sinx-1\right)=m\left(1-sinx\right)\left(1+cosx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\Rightarrow x=\dfrac{\pi}{2}\\cos2x+3m.sinx+sinx-1=m\left(1+sinx\right)\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 5 nghiệm khác nhau trên khoảng đã cho thỏa mãn \(sinx\ne1\)
Xét (1):
\(\Leftrightarrow1-2sin^2x+3msinx+sinx-1=m+m.sinx\)
\(\Leftrightarrow2sin^2x-sinx-2m.sinx+m=0\)
\(\Leftrightarrow sinx\left(2sinx-1\right)-m\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx-m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\Rightarrow x=\dfrac{\pi}{6};\dfrac{5\pi}{6}\\sinx=m\left(2\right)\end{matrix}\right.\)
\(\Rightarrow\left(2\right)\) có 3 nghiệm khác nhau trên \(\left(-\dfrac{\pi}{2};2\pi\right)\)
\(\Leftrightarrow-1< m< 0\)


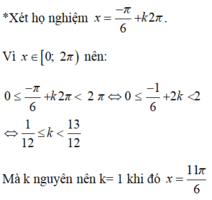

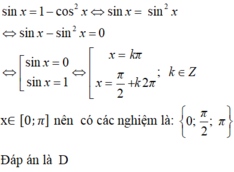


Xét f(x) = cos2x - sinx + 2 trên các khoảng