Một hệ bao gồm hai thấu kính (L1 )và (L2) đồng trục có tiêu điểm ảnh chính của (L1) trùng với tiểu điểm chính của (L2). Chiếu một chùm tia sáng song song tới (L1) theo bất kì.
Chứng minh chùm tia ló ra khỏi (L2) cũng là chùm tia ló song song.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ đường đi của chùm tia sáng ứng với các trường hợp:
+ (L1) và (L2) đều là thấu kính hội tụ:
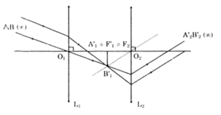
+ L1 là thấu kính hội tụ; L2 là thấu kính phân kì:
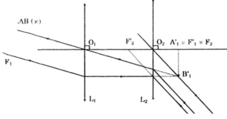
+ L1 là thấu kính phân kì; L2 là thấu kính hội tụ:
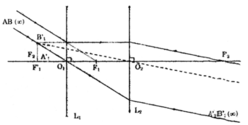

Đáp án A
Chiếu một chùm tia sáng song song tới L1 thì chùm tia ló ra khỏi L2 là chùm tia song song

Đáp án C
Ta có sơ đồ tạo ảnh:
A B → A ' B ' → A ' ' B ' ' d 1 d 1 ' d 2 d 2 '
Chùm sáng tới L 1 là chùm sáng song song ↔ d 1 = ∞ → d ' 1 = f 1
Chùm sáng tới L 2 cũng là chùm sáng song song ↔ d ' 2 = ∞ → d 2 = f 2
Vậy khoảng cách giữa hai thấu kính là a = f 1 + f 2 = 10 c m

Chọn đáp án C
Ta có sơ đồ tạo ảnh A B → A ' B ' → A " B " d 1 d 1 ' d 2 d 2 '
Chùm sáng tới L 1 là chùm sáng song song ↔ d 1 = ∞ → d 1 ' = f 1
Chùm sáng ra khỏi L 2 cũng là chùm song song ↔ d ' 2 = ∞ → d 2 = f 2
Vậy khoảng cách giữa hai thấu kính là a = f 1 + f 2 = 10 c m .

Đáp án C
+ Theo đề bài thì: F 1 ' ≡ F 2
+ Mà L 2 là thấu kính phân kì nên F 2 thuộc O 2 y
® T thuộc O 2 y

Đáp án A
Nếu L1 là thấu kính phân kì và L2 là thấu kính hội tụ thì T thuộc xO 1

Đáp án B
Nêu L1 là thấu kính hội tụ và L2 là thấu kính phân kì thì T thuộc O 2 y

Đáp án D
Nếu L1 và L2 đều là thấu kính phân kì thì không tồn tại T
Sơ đồ tạo ảnh của hệ hai thấu kính đồng trục:
Trong đó:
Hệ gồm hai thấu kính L1 và L2 đồng trục có tiêu điểm ảnh chính của (L1) trùng với tiêu điểm vật chính của L2 ⇒ l = O1O2 = f1 + f2
Chùm tia sáng tới song song: d1 = ∞ ⇒ d'1 = f1
⇒ d2 = l - d'1 = f2 ⇒ d'2 = ∞
⇒ chùm tia ló ra khỏi (L2) cũng là chùm tia song song.