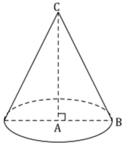
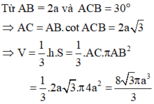Trong không gian cho tam giác ABC vuông tại A có AB=a và BC=2a. Quay tam giác ABC xung quanh cạnh AB ta thu được khối nón có thể tích bằng
A. π a 3 .
B. 3 π a 3 .
C. 3 3 π a 3 .
D. 2 3 π a 3 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

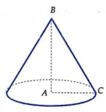

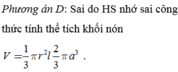

Đáp án A

Ta có chiều cao của khối nón bán kính hình tròn đáy lần lượt là
h = AB = a và r = AC = ![]()
Suy ra thể tích của khối nón là 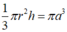
Phân tích phương án nhiễu.
Phương án B: Sai do HS thiếu 1 3 trong công thức tính thể tích.
Phương án C: Sai do HS xác định h = a 3 và bán kính đáy r = a nên
![]()
Phương án D: Sai do HS nhớ sai công thức tính thể tích khối nón
![]()

Chọn A.
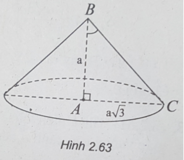
(h.2.63) Độ dài đường sinh l bằng độ dài cạnh BC của tam giác vuông ABC.
Theo định lý Py-ta-go, ta có:
BC 2 = AB 2 + AC 2 = a 2 + 3 a 2 = 4 a 2
⇒ BC = 2a.
Vậy độ dài đường sinh của hình nón là l = 2a.

Đáp án A
Khi quay tam giác ABC quanh cạnh AC ta được khối nón có chiều cao là AC, bán kính đáy là AB