Khai triển đa thức 1 - 3 x 20 = a 0 + a 1 x + a 2 x 2 + . . . + a 20 x 20 . Tính tổng S = a 0 + 2 a 1 + 3 a 2 + . . . + 21 a 20
A. 4 20
B. 4 21
C. 4 22
D. 4 23
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

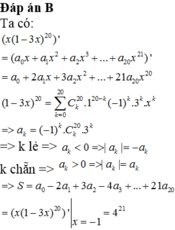

Gặp dạng hệ số đằng trước giống chỉ số của số hạng thế này thì cứ đạo hàm
\(\left(1+x+x^2\right)^{20}=a_0+a_1x+a_2x^2+...+a_{40}x^{40}\)
Đạo hàm 2 vế:
\(\Rightarrow20\left(1+x+x^2\right)^{19}\left(1+2x\right)=a_1+2a_2x+3a_3x^2+...+40a_{40}x^{39}\)
Cho \(x=1\) ta được:
\(20.3^{19}.3=a_1+2a_2+3a_3+...+40a_{40}\)
\(\Rightarrow T=20.3^{20}\)

\(A=\left(x-a\right)^2.\left(x+a\right)^2\) =\(\left[\left(x-a\right)\left(x+a\right)\right]^2\)
= \(\left(x^2-a^2\right)^2\) = \(x^4-2x^2a^2+a^4\)
\(B=\left(1+a\right)\left(1-a\right)\left(1+a^2\right)\left(1+a^4\right)\) = \(\left(1-a^2\right)\left(1+a^2\right)\left(1+a^4\right)\)
= \(\left(1-a^4\right)\left(1+a^4\right)\) = \(1-a^8\)

A(0)=9 => a.0^2+b.0+c = 0
=> c=0
A(1)= a.1^2+b*1+0=20
=> a + b = 20(1)
A(-2)=7 => a(-2)^2+b*(-2)+0=7
=> 4a-2b=7
=> 2(2a-b)=7
=> 2a-b=3,5(2)
Từ (1) và (2) suy ra
a+b+2a-b=23,5
3a=23,5
=> a=47/6
=> b= 73/6
A(0) = 9 suy ra a . 0^2 + b * 0 + c = 0
Suy ra c = 0
A(1) = a . 1^2 + b*1 + 0 = 20
Suy ra a + b = 20 (1)
A(-2) = 7 suy ra a (-2)^2 + b * (-2) + 0 = 7
Suy ra 4a - 2b = 7
Suy ra 2( 2a - b )
Suy ra 2a - b = 3,5 (2)
Từ (1) và (2) suy ra a + b + 2a -b = 23,5
3a = 23,5
Suy ra a = 47/6
b = 73/6

Câu hỏi của Nguyễn Minh Vũ - Toán lớp 7 - Học toán với OnlineMath
Bạn tham khảo ở link trên.

Ta có:
f ( 1 ) = \(a_0+a_1+....+a_{2017}\)
mà f ( x) = \(\left(x+2\right)^{2017}\)
=> \(S=f\left(1\right)=3^{2017}\)

Bài 2:
a) \(x^2+y^2-9-2xy\)
\(=\left(x^2-2xy+y^2\right)-3^2\)
\(=\left(x-y\right)^2-3^2\)
\(=\left(x-y-3\right)\left(x-y+3\right)\)
b) \(4x^2-5x-9\)
\(=4x^2+4x-9x-9\)
\(=4x\left(x+1\right)-9\left(x+1\right)\)
\(=\left(x+1\right)\left(4x-9\right)\)
\(\left(2x-3\right)^2-\left(4x-1\right)\left(x+2\right)=4x^2-12x+9-4x^2-7x+2=-19x+11\)
\(\left(3x+2\right)\left(3x-2\right)-\left(3x-1\right)^2=9x^2-4-9x^2+6x-1=6x-5\)
\(x^2+y^2-9-2xy=\left(x-y\right)^2-9=\left(x-y-3\right)\left(x-y+3\right)\)
\(4x^2-5x-9=\left(4x-9\right)\left(x+1\right)\)
\(\left(x-3\right)^2-\left(x-1\right)\left(x-2\right)=5\Leftrightarrow x^2-6x+9-x^2+3x-2=5\)
\(\Leftrightarrow-3x=-2\Leftrightarrow x=x=\frac{2}{3}\)
\(3x^2+5x-8=0\Leftrightarrow\left(x-1\right)\left(3x+8\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=-\frac{8}{3}\end{cases}}\)

Bài 1:
a, x2-3xy-10y2
=x2+2xy-5xy-10y2
=(x2+2xy)-(5xy+10y2)
=x(x+2y)-5y(x+2y)
=(x+2y)(x-5y)
b, 2x2-5x-7
=2x2+2x-7x-7
=(2x2+2x)-(7x+7)
=2x(x+1)-7(x+1)
=(x+1)(2x-7)
Bài 2:
a, x(x-2)-x+2=0
<=>x(x-2)-(x-2)=0
<=>(x-2)(x-1)=0
<=>\(\orbr{\begin{cases}x-2=0\\x-1=0\end{cases}}\)<=>\(\orbr{\begin{cases}x=2\\x=1\end{cases}}\)
b, x2(x2+1)-x2-1=0
<=>x2(x2+1)-(x2+1)=0
<=>(x2+1)(x2-1)=0
<=>x2+1=0 hoặc x2-1=0
1, x2+1=0 2, x2-1=0
<=>x2= -1(loại) <=>x2=1
<=>x=1 hoặc x= -1
c, 5x(x-3)2-5(x-1)3+15(x+2)(x-2)=5
<=>5x(x-3)2-5(x-1)3+15(x2-4)=5
<=>5x(x2-6x+9)-5(x3-3x2+3x-1)+15x2-60=5
<=>5x3-30x2+45x-5x3+15x2-15x+5+15x2-60=5
<=>30x-55=5
<=>30x=55+5
<=>30x=60
<=>x=2
d, (x+2)(3-4x)=x2+4x+4
<=>(x+2)(3-4x)=(x+2)2
<=>(x+2)(3-4x)-(x+2)2=0
<=>(x+2)(3-4x-x-2)=0
<=>(x+2)(1-5x)=0
<=>\(\orbr{\begin{cases}x+2=0\\1-5x=0\end{cases}}\)<=>\(\orbr{\begin{cases}x=-2\\-5x=-1\end{cases}}\)<=>\(\orbr{\begin{cases}x=-2\\x=\frac{-1}{-5}\end{cases}}\)<=>\(\orbr{\begin{cases}x=-2\\x=\frac{1}{5}\end{cases}}\)
Bài 3:
a, Sắp xếp lại: x3+4x2-5x-20
Thực hiện phép chia ta được kết quả là x2-5 dư 0
b, Sau khi thực hiện phép chia ta được :
Để đa thức x3-3x2+5x+a chia hết cho đa thức x-3 thì a+15=0
=>a= -15