Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích V của khối chóp có thể tích lớn nhất.
A. V = 144
B. V = 576 2
C. V = 576
D. V = 144 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
7 tháng 12 2018
Đúng(0)
Những câu hỏi liên quan
CM
8 tháng 3 2019
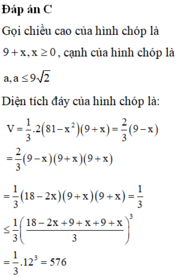
Đáp án C
Gọi chiều cao của hình chóp là 9 + x , x ≥ 0 , cạnh của hình chóp là a , a ≤ 9 2
Diện tích đáy của hình chóp là: V = 1 3 .2 81 − x 2 9 + x = 2 3 9 − x = 2 3 9 − x 9 + x 9 + x
= 1 3 18 − 2 x 9 + x 9 + x = 1 3 ≤ 1 3 18 − 2 x + 9 + x + 9 + x 3 3 = 1 3 .12 3 = 576
CM
24 tháng 7 2019
Đáp án B
Ta có: R = S A 2 2 S O = 9
Suy ra S O 2 + O A 2 S O = 18
Mặt khác V S . A B C D = 1 3 S O . S A B C D = 1 3 S O . A C 2 2 = 2 3 S O . O A 2
= 2 3 S O . 18 S O − S O 2 . đặt S O = t 0 < t < 18 , xét hàm số
f t = 2 3 t 2 18 − t = 8 3 . t 2 . t 2 18 − t ≤ 8 3 t + 18 − t 3 3 = 576
CM
14 tháng 8 2018
Đáp án D
Xét khối chóp tứ giác đều S.ABCD có chiều aco S H = h , A B = x
Bán kính mặt cầu ngoại tiếp khối chóp S.ABCD là R = S A 2 2 × S H = 3 ⇔ S A 2 = 6 × S H
Tam giác SAH vuông tại H, ta có S A 2 = S H 2 + A H 2 = S H 2 + A B 2 2 = h 2 + x 2 2
Suy ra h 2 + x 2 2 = 6 h ⇔ x 2 = 12 h − 2 h 2 .
Thể tích khối chóp S.ABCD là V = 1 3 . S H . S A B C D
Khi đó V = 1 3 h . x 2 = 2 3 h 6 h − h 2 = 2 3 6 h 2 − h 3 ≤ 64 3 (khảo sát hàm số)