Cho tứ diện ABCD, M là điểm thuộc BC sao cho MC = 2MB. N, P lần lượt là trung điểm của BD và AD. Điểm Q là giao điểm của AC với (MNP). Tính QA/QC.
A. Q A Q C = 1 2
B. Q A Q C = 2
C. Q A Q C = 2 3
D. Q A Q C = 3 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: MP cắt BC tại E mà BC thuộc (BCD)
Nên: E là giao điểm của đường thẳng MP với mặt phẳng (BCD).
b) Ta có: EN cắt CD tại Q mà EN thuộc (MNP)
Nên: Q là giao điểm của đường thẳng CD với mặt phẳng (MNP).
c) Ta có: P thuộc (MNP) và (ACD)
Q thuộc (MNP) và (ACD)
Nên PQ là giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
d) △ACN có: \(\dfrac{AP}{AC}=\dfrac{AG}{AN}=\dfrac{2}{3}\)
Suy ra: PG // CN
Do đó: △PIG đồng dạng với △NIC
Do đó: C, I, G thẳng hàng.

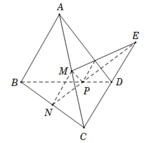
Chọn mặt phẳng phụ chứa CD là (BCD)
Do NP không song song CD nên NP cắt CD tại E
Điểm E ∈ N P ⇒ E ∈ M N P .
Vậy C D ∩ M N P tại E.
Chọn A

Đáp án A
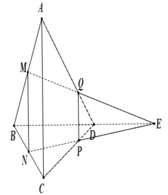
Gọi ![]() thì Q là giao điểm của (MNP) và AD.
thì Q là giao điểm của (MNP) và AD.
Áp dụng định lí Menelaus trong ∆ B C D ta có:
![]()
![]()
Áp dụng định lí Menelaus trong ∆ ABD ta có:
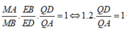
![]()
NP là đường trung bình của ∆ACD ⇒ NP // AB, mà AB ⊂ (ABC) ⇒NP // (ABC)
P ∈ (MNP) ∩ (ACD) (1)
Trong mặt phẳng (BCD) gọi J = MN ∩ CD, có
J ∈ (MNP) ∩ (ACD) (2)
Từ (1) và (2) : (MNP) ∩ (ACD) = JP
Trong mặt phẳng (ACD) gọi Q = JP ∩ AC. Có:
⇒ Q = AC ∩ (MNP). Có:
⇒MQ // NP // AB
Theo định lí Ta – lét có
Kết luận:
Đáp án A