Lớp 10X có 25 học sinh, chia lớp 10X thành hai nhóm A và B sao cho mỗi nhóm đều có học sinh nam và học sinh nữ. Chọn ngẫu nhiên hai học sinh từ hai nhóm, mỗi nhóm một học sinh. Tính xác suất để chọn được hai học sinh nữ. Biết rằng, trong nhóm A có đúng 9 học sinh nam và xác suất chọn được hai học sinh nam bằng 0,54. A. 0,42. B. 0,04. C. 0,46. D....
Đọc tiếp
Lớp 10X có 25 học sinh, chia lớp 10X thành hai nhóm A và B sao cho mỗi nhóm đều có học sinh nam và học sinh nữ. Chọn ngẫu nhiên hai học sinh từ hai nhóm, mỗi nhóm một học sinh. Tính xác suất để chọn được hai học sinh nữ. Biết rằng, trong nhóm A có đúng 9 học sinh nam và xác suất chọn được hai học sinh nam bằng 0,54.
A. 0,42.
B. 0,04.
C. 0,46.
D. 0,23.
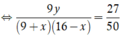
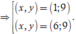
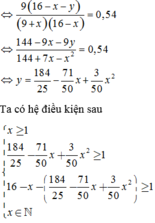
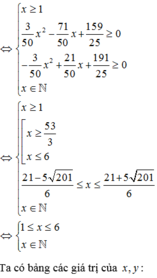
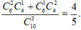
Đáp án B
Gọi số học sinh nữ trong nhóm A là x ( x ∈ ℕ * )
Gọi số học sinh nam trong nhóm B là y ( y ∈ ℕ * ) .
=> Số học sinh nữ trong nhóm B là 25 – 9 – x = 16 – x – y => x + y < 16
Khi đó, Nhóm A: 9 nam, x nữ và nhóm B: y nam, 16 – x – y nữ.
Xác suất để chọn được hai học sinh nam là
C 9 1 . C y 1 C 9 + x 1 . C 25 - 9 - x 1 = 0 , 54
⇔ 9 y ( 9 + x ) ( 16 - x ) = 27 50 .
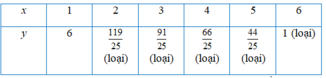
⇒ y = 30 50 ( 9 + x ) ( 16 - x ) ⇒ x < 16 .
Vì y ∈ ℕ * ⇒ 3 50 ( 9 + x ) ( 16 - x ) ∈ N * .
=> (x, y) = {(1; 9), (6; 9), (11; 6)}.
Mặt khác x + y < 16
( Khi chia nhóm thì A,B có vai trò như nhau nên có 2 cặp thỏa mãn )
Vậy xác suất để chọn đươc hai học sinh nữ là 0,04.