Cho đa giác đều có 15 đỉnh. Gọi M là tập tất cả các tam giác có ba đỉnh là ba đỉnh của đa giác đã cho. Chọn ngẫu nhiên một tam giác thuộc tập M, tính xác suất để tam giác được chọn là một tam giác cân nhưng không phải là tam giác đều. A.
73
91
B.
18
91
C.
8
91
D.
18
19
...
Đọc tiếp
Cho đa giác đều có 15 đỉnh. Gọi M là tập tất cả các tam giác có ba đỉnh là ba đỉnh của đa giác đã cho. Chọn ngẫu nhiên một tam giác thuộc tập M, tính xác suất để tam giác được chọn là một tam giác cân nhưng không phải là tam giác đều.
A. 73 91
B. 18 91
C. 8 91
D. 18 19
. Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n?
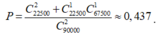
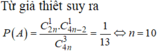
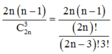
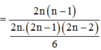
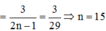
Đáp án B
Số phần tử của tập hợp M là: C 15 3
Gọi O là tâm đường tròn ngoại tiếp của đa giác đều, Xét một đỉnh A bất kỳ của đa giác: Có 7 cặp đỉnh của đa giác đối xứng với nhau qua đường thẳng OA, hay có 7 tam giác cân tại đỉnh A. Như vậy, với mỗi một đỉnh của đa giác có 7 tam giác nhận nó làm đỉnh tam giác cân.
Số tam giác đều có 3 đỉnh là các đỉnh của đa giác là 15 3 = 5 tam giác.
Tuy nhiên, trong các tam giác cân đã xác định ở trên có cả tam giác đều, do mọi tam giác đều thì đều cân tại 3 đỉnh nên tam giác đều được đếm 3 lần.
Suy ra, số tam giác cân nhưng không phải tam giác đều có 3 đỉnh là 3 đỉnh của đa giác đã cho là: 7.15 – 3.5 = 90
Do đó xác suất cần tìm là P = 90 C 15 3 = 18 91 .