Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
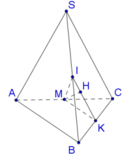
Gọi K là trung điểm của BC.
nên dễ dàng nhận thấy trung điểm I của SB là tâm mặt cầu ngoại tiếp chóp SABC.
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, ta có MA = MB = MC.
mặt khác IA = IB = IC, do đó IM là trục của đường tròn ngoại tiếp tam giác ABC hay IM ⊥ (ABC)
Xét tam giác vuông IMA ta có
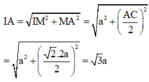
Vậy diện tích mặt cầu ngoại tiếp chóp SABC là
Đáp án A.
Theo giả thiết ta có SO ⊥ (ABC). Gọi D là điểm đối xưng với B qua O
=> ABCD là hình vuông => AB//CD
=> d(AB;SC) = d(AB;(SCD)) = d(E;(SCD)) = 2d(O;(SCD))(Với E, F lần lượt là trung điểm của AB và CD).
Áp dung tính chất tứ diện vuông cho tứ diện OSCD ta có:
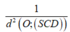
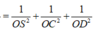
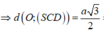
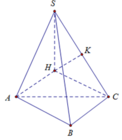
Đáp án B
Dựng hình vuông ABCH
Ta có: A B ⊥ A H A B ⊥ S A ⇒ A B ⊥ S H , tương tự B C ⊥ S H
Do đó S H ⊥ A B C
Lại có A H / / B C ⇒ d A ; S B C = d H ; S B C
Dựng H K ⊥ S C ⇒ d H ; S B C − H K = a 2
Do đó 1 S H 2 = 1 H K 2 − 1 H C 2 ⇒ S H = a 6 .
Tứ giác ABCH nội tiếp nên R S . A B C = R S . A B C H = S H 2 4 + r 2 d
= S H 2 4 + A C 2 2 = a 3 ⇒ S = 4 π R 2 = 12 π a 2 .
Đáp án C
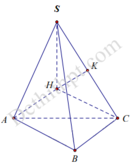
Dựng hình vuông ABCH
Ta có A B ⊥ A H A B ⊥ S A ⇒ A B ⊥ S H , tương tự B C ⊥ S H
Do đó S H ⊥ A B C
Lại có A H / / B C ⇒ d A ; S B C = d H ; S B C
Dựng H K ⊥ S C ⇒ d H ; S B C = H K = a 2
Do đó 1 S H 2 = 1 H K 2 − 1 H C 2 ⇒ S H = a 30 5
Tứ giác ABCH nội tiếp nên R S . A B C = R S . A B C H = S H 2 4 + r d 2
= S H 2 4 + A C 2 2 = a 2 ⇒ S = 4 π R 2 = 8 π a 2
Đáp án A
Gọi K là trung điểm của BC.
Do SAB ^ = SCB ^ = 90 o nên dễ dàng nhận thấy trung điểm I của SB là tâm mặt cầu ngoại tiếp chóp SABC.
Gọi M là trung điểm của AC.
Tam giác ABC vuông tại B, ta có MA = MB = MC , mặt khác IA = IB = IC , do đó IM là trục của đường tròn ngoại tiếp tam giác ABC hay IM ⊥ ABC
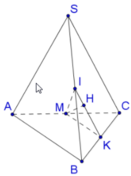
ĐÁP ÁN: D