Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh AB= a 6 , cạnh SC=4 3 a Hai mặt phẳng (SAD) và (SAC) cùng vuông góc với mặt phẳng (ABCD) và M là trung điểm của SC. Tính góc giữa đường thẳng BM và mặt phẳng (ACD)
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
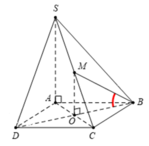
Gọi O là tâm của hình vuông A B C D ⇒ O M ⊥ A B C D .
Suy ra M B ; A C D ^ = M B ; A B C D ^ = M B ; O B ^ = M B O ^
Tam giác SAC vuông ⇒ S A = S C 2 − A C 2 = 6 a ⇒ O M = 3 a
Tam giác OMB vuông tại O, có tan M B O ^ = O M O B = 3 a 3 a = 3 .
Vậy góc giữa đường thẳng BM và mp (ACD) là 60 ∘ .

Chọn đáp án C
Ta có
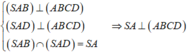
⇒ A C là hình chiếu của SC trên mặt phẳng (ABCD)
![]()
Lại có ABCD là hình vuông cạnh a nên A C = a 2
Tam giác SAC vuông tại A nên S A = A C . tan S C A ⏜ = a 6
Vậy thể tích khối chóp S.ABCD là V A B C D = a 3 6 3 (đvtt).

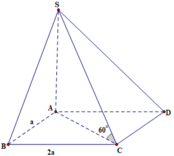
+Vì S A B ⊥ A B C D , S A D ⊥ A B C D mà S A B ∩ S A D = S A nên S A là đường cao của khối chóp
+ Xét tam giác vuông S A C
S A = tan 60 o . A C = 3 . a . 5 = a 15