Trong không gian Oxyz, cho điểm M (1;1;2). Mặt phẳng (P) qua M cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất. Gọi là một véc tơ pháp tuyến của (P). Tính S=a³-2b. A. S=0. B. S=-3. C. S=6. ...
Đọc tiếp
Trong không gian Oxyz, cho điểm M (1;1;2). Mặt phẳng (P) qua M cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất. Gọi 
là một véc tơ pháp tuyến của (P). Tính S=a³-2b.
A. S=0.
B. S=-3.
C. S=6.
D. S=-15/8
Chọn A
Mặt phẳng (P) cắt các tia Ox, Oy, Oz lần lượt tại A, B, C nên A (a;0;0), B (0;b;0), C (0;0;c) (a, b, c>0).
Phương trình mặt phẳng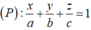
+ Mặt phẳng (P) qua M nên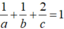
+ Thể tích khối tứ diện OABC: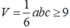
Thể tích khối tứ diện OABC nhỏ nhất khi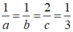
suy ra a=3, b=3, c=6.
Vậy S = 0