Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z. z ¯ = 1 và |z - 3 + i|. Tìm số phần tử của S
A. 1.
B. 2.
C. 3.
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Đặt \(z=a+bi(a,b\in\mathbb{R})\)
Từ \(z\overline{z}=1\Rightarrow a^2+b^2=1\)
Do đó tập hợp các điểm biểu diễn số phức $z$ nằm trên đường tròn tâm \(O(0;0)\) bán kính \(R=1\)
Lại có:
\(|z+\sqrt{3}+i|=m(m\geq 0)\)
\(\Leftrightarrow |(a+\sqrt{3})+i(b+1)|=m\)
\(\Leftrightarrow (a+\sqrt{3})^2+(b+1)^2=m^2\)
Do đó tập hợp các điểm biểu diễn số phức $z$ nằm trên đường tròn tâm \(I(-\sqrt{3}; -1)\) bán kính \(R'=m\)
Để số phức $z$ tồn tại duy nhất thì \((O); (I) \) phải tiếp xúc trong hoặc tiếp xúc ngoài.
Nếu \((O); (I)\) tiếp xúc ngoài:
\(\Rightarrow OI=R+R'\Leftrightarrow 2=1+m\Leftrightarrow m=1\)
Nếu \((O),(I)\) tiếp xúc trong.
TH1: \((O)\) nằm trong $(I)$
\(OI+R=R'\Leftrightarrow 2+1=m\Leftrightarrow m=3\)
TH2: \((I)\) nằm trong $(O)$
\(OI+R'=R\Leftrightarrow 2+m=1\Leftrightarrow m=-1\) (loại vì \(m\geq 0\) )
Do đó \(S=\left\{1;3\right\}\) hay số phần tử của S là 2.

Cách 1 (cách hình học): Gọi M ( x ; y ) x . y ∈ ℝ là điểm biểu diễn của số phức z thỏa mãn yêu cầu bài toán.
Có: z + 2 m = m + 1 ≥ 0
TH1: m + 1 = 0 ⇔ ⇔ m = - 1 ⇒ z = 2 (loại) vì không thỏa mãn phương trình: z - 1 = z - i
TH2: m + 1 > 0 ⇔ m > - 1
Theo bài ra ta có:
z - 1 = z - i z + 2 m = m + 1 ⇔ x - 1 + y i = x + y - 1 i x + 2 m + y i = m + 1 ⇔ x - 1 2 + y 2 = x 2 + y - 1 2 x + 2 m 2 + y 2 = m + 1 2 ⇔ x - y = 0 1 x + 2 m 2 + y 2 = m + 1 2 2 *
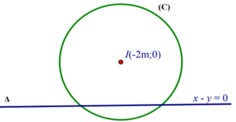
Từ (1) suy ra: tập hợp điểm M(x;y) biểu diễn của số phức z là đường thẳng: ( ∆ ) : x - y = 0
Từ (2) suy ra: tập hợp điểm M(x;y) biểu diễn của số phức z là đường tròn
( C ) : T â m I ( - 2 m ; 0 ) b k R = m + 1
Khi đó: M ∈ ∆ ∩ ( C ) ⇒ số giao điểm M chính là số nghiệm của hệ phương trình (*).
Để tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn ycbt ⇔ ( C ) cắt ∆ tại hai điểm phân biệt
⇔ d I , ∆ < R ⇔ - 2 m 2 < m + 1 m + 1 > 0 ⇔ - m + 1 < 2 m < m + 1 m + 1 > 0 ⇔ 1 - 2 < m < 1 + 2 m > - 1
Vì m ∈ ℝ ⇒ m ∈ S 0 ; 1 ; 2 . Vậy tổng các phần tử của S là 0+1+2=3.
Cách 2 (cách đại số):
Giả sử: z = x + y i x ; y ∈ ℝ
Có: z + 2 m = m + 1 ≥ 0
TH1: m + 1 = 0 ⇔ ⇔ m = - 1 ⇒ z = 2 (loại) vì không thỏa mãn phương trình: z - 1 = z - i
TH2: m + 1 > 0 ⇔ m > - 1 (1)
Theo bài ra ta có:
z - 1 = z - i z + 2 m = m + 1 ⇔ x - 1 + y i = x + y - 1 i x + 2 m + y i = m + 1 ⇔ x - 1 2 + y 2 = x 2 + y - 1 2 x + 2 m 2 + y 2 = m + 1 2 ⇔ y = x x + 2 m 2 + x 2 = m + 1 2 ⇔ y = x 2 x 2 + 4 m x + 3 m 2 - 2 m + 1 = 0 *
Để tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn ycbt PT (*) có 2 nghiệm phân biệt
⇔ ∆ ' = 4 m 2 - 2 ( 3 m 2 - 2 m - 1 ) = 2 - m 2 + 2 m + 1 > 0 ⇔ 1 - 2 < m < 1 + 2 ( 2 )
Kết hợp điều kiện (1) và (2), m ∈ ℝ ⇒ m ∈ S = 0 ; 1 ; 2
Vậy tổng các phần tử của S là: 0+1+2=3
Chọn đáp án D.

Đặt \(z=x+yi\Rightarrow w=\dfrac{1}{\sqrt{x^2+y^2}-x-yi}=\dfrac{\sqrt{x^2+y^2}-x+yi}{\left(\sqrt{x^2+y^2}-x\right)^2+y^2}\)
\(\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{\left(\sqrt{x^2+y^2}-x\right)^2+y^2}=\dfrac{1}{8}\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{2x^2+2y^2-2x\sqrt{x^2+y^2}}=\dfrac{1}{8}\)
\(\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{\sqrt{x^2+y^2}\left(\sqrt{x^2+y^2}-x\right)}=\dfrac{1}{4}\Rightarrow\dfrac{1}{\sqrt{x^2+y^2}}=\dfrac{1}{4}\)
\(\Rightarrow x^2+y^2=16\)
\(\Rightarrow\) Tập hợp \(z_1;z_2\) là đường tròn tâm O bán kính \(R=4\)
Gọi M, N lần lượt là điểm biểu diễn \(z_1;z_2\), do \(\left|z_1-z_2\right|=2\Rightarrow MN=2\)
Gọi \(P\left(0;5\right)\) và Q là trung điểm MN
\(\Rightarrow P=MP^2-NP^2=\overrightarrow{MP}^2-\overrightarrow{NP}^2=\left(\overrightarrow{MP}-\overrightarrow{NP}\right)\left(\overrightarrow{MP}+\overrightarrow{NP}\right)\)
\(=2\overrightarrow{MN}.\overrightarrow{PQ}=2\overrightarrow{MN}\left(\overrightarrow{PO}+\overrightarrow{OQ}\right)=2\overrightarrow{MN}.\overrightarrow{PO}=2MN.PO.cos\alpha\)
Trong đó \(\alpha\) là góc giữa \(MN;PO\)
Do MN, PO có độ dài cố định \(\Rightarrow P_{max}\) khi \(cos\alpha_{max}\Rightarrow\alpha=0^0\Rightarrow MN||PO\)
Mà MN=2 \(\Rightarrow M\left(\sqrt{15};-1\right);N\left(\sqrt{15};1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{PM}=\left(\sqrt{15};-6\right)\\\overrightarrow{PN}=\left(\sqrt{15};-4\right)\end{matrix}\right.\)
\(\Rightarrow P_{max}=PM^2-PN^2=15+36-\left(15+16\right)=20\)

Đáp án A
Phương pháp: Đặt ![]()
Biến đổi để phương trình trở thành ![]()
Cách giải: 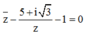
![]()
Đặt ![]() , ta có:
, ta có:
![]()
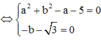
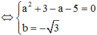

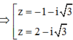 => Tổng giá trị tất cả các phần tử của S bằng
1
-
2
3
i
=> Tổng giá trị tất cả các phần tử của S bằng
1
-
2
3
i
Đáp án A
Đặt z=x+yi
Ta có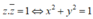 suy ra tập biểu diễn số phức z là đường tròn tâm M(0;0) bán kính R=1
suy ra tập biểu diễn số phức z là đường tròn tâm M(0;0) bán kính R=1
Để tồn tại duy nhất số phức z thì 2 đường tròn phải tiếp xúc với nhau suy ra MN=R+r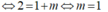
Vậy tập S chỉ có 1 giá trị của m