[1/18+2/17+.......18/1+18] : [1/18+1/17+...+1/1]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CT
0
NT
0
3 tháng 1 2016
Xét tử:
tử = 1/18 + 2/17 + 3/16 + ... + 18/1 + (1+1+1+...+1)(18 số 1)
=(1/18 + 1)+(2/17 + 1)+...+(18/1 + 1)
=19/18 + 19/17 + ... + 19/1
=19(1/18 + 1/17 + ... + 1/1)
Nên tử/ mẫu =19
DT
2
24 tháng 3 2017
Nếu nghĩ kĩ thì thấy bài này cũng đơn giản thôi.Thử xem cách giải của mk nè:
Giải: Ta có: A=\(\frac{17^{18}+1}{17^{19}+1}\) B=\(\frac{17^{17}+1}{17^{18}+1}\)
17A=\(\frac{17^{19}+17}{17^{19}+1}\) 17B=\(\frac{17^{18}+17}{17^{18}+1}\)
17A=\(\frac{\left(17^{19}+1\right)+16}{17^{19}+1}\) 17B=\(\frac{\left(17^{18}+1\right)+16}{17^{18}+1}\)
17A=\(\frac{17^{19}+1}{17^{19}+1}+\frac{16}{17^{19}+1}\) 17B=\(\frac{17^{18}+1}{17^{18}+1}+\frac{16}{17^{18}+1}\)
17A=\(1+\frac{16}{17^{19}+1}\) 17B= \(1+\frac{16}{17^{18}+1}\)
Lại có: 1719+1>1718+1
Suy ra:\(\frac{16}{17^{19}+1}< \frac{16}{17^{18}+1}\)
17A<17B
A<B
Vậy A<B
10 tháng 4 2022
\(\text{Ta có:}\frac{17^{18}+1}{17^{19}+1}\)
\(\Rightarrow17A=\frac{17^{19}+1+16}{17^{19}+1}\)
\(\Rightarrow17A=1+\frac{16}{17^{19}+1}\)
\(B=\frac{17^{17}+1}{17^{18}+1}\)
\(\Rightarrow17B=\frac{17^{18}+1+16}{17^{18}+1}\)
\(\Rightarrow17B=1+\frac{16}{17^{18}+1}\)
\(\text{Vì }\frac{16}{17^{19}+1}< \frac{16}{17^{18}+1}\)
\(\Rightarrow17A< 17B\)
\(\Rightarrow A< B\)
DT
0
D
1
BN
20 tháng 5 2018
Ta có công thức :
\(\frac{a}{b}< \frac{a+c}{b+c}\left(\frac{a}{b}< 1;a,b,c\inℕ^∗\right)\)
Áp dụng vào ta có :
\(A=\frac{17^{18}+1}{17^{19}+1}< \frac{17^{18}+1+16}{17^{19}+1+16}\)
\(=\frac{17^{18}+17}{17^{19}+17}\)
\(=\frac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}\)
\(\Leftrightarrow\frac{17^{17}+1}{17^{18}+1}\)'
\(\Rightarrow=B\)
Vậy \(A< B\)
16 tháng 4 2021
A=(17^18+1)/(17^19+1)
17A=17(17^18+1)/17^19+1=17^19+17/17^19+1
17A=(17^19+1)+16/(17^19+1)=1+16/17^19+1
B=(17^17+1)/(17^18+1)
17B=17(17^17+1)/17^18+1=17^18+17/17^18+1
17B=(17^18+1)+16/(17^18+1)=1+16/17^18+1
Từ (1) và (2)⇒1+16/17^19+1<1+16/17^18+1
=> 17A<17B
Hay A<B
Vậy A<B
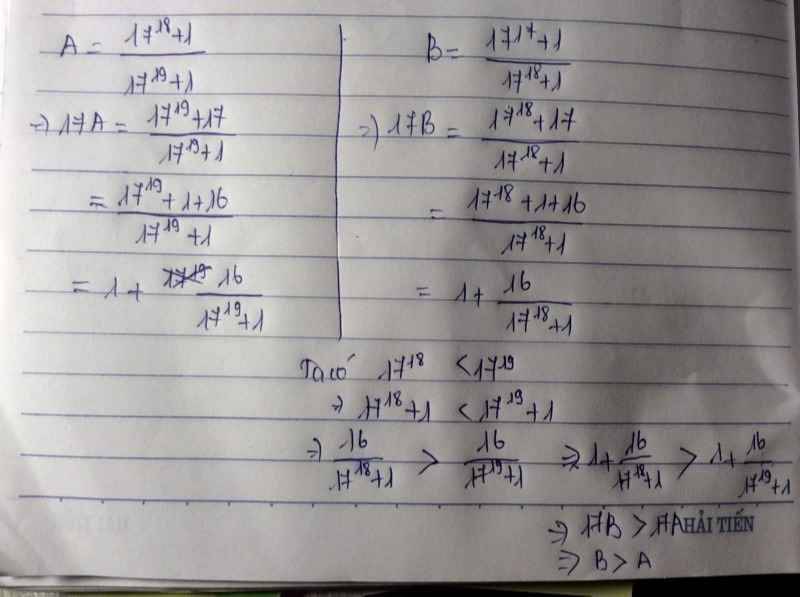
= 19 cách giải thì chờ OLM duyệt
nhanhnhanh giup mk vs