Cho tam giác ABC cân tại A có A ^ = 66 ° nội tiếp đường tròn (O) . Trong các cung nhỏ AB, BC, CA thì cung nào là cung lớn nhất?
A. AB
B. AC
C. BC
D. AB, AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C.
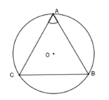
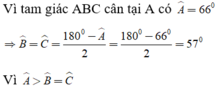
nên theo mối liên hệ giữa cạnh và góc trong tam giác ta có:


góc ABC=góc ACB=(180-66)/2=114/2=57 độ
=>góc BAC>góc ABC=góc ACB
=>Trong các cung nhỏ AB,BC,CA thì cung lớn nhất là cung BC

a)Xét tứ giác MBOC có
\(\widehat{OBM}\) và \(\widehat{OCM}\) là hai góc đối
\(\widehat{OBM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MBOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)


a) Do AB // DE nên \(\widebat{AE}=\widebat{BD}\Rightarrow\widebat{AE}+\widebat{DC}=\widebat{BD}+\widebat{DC}=\widebat{BC}\)
Ta có \(\widehat{MIC}\) là góc có đỉnh nằm trong đường tròn nên \(\widehat{MIC}=\frac{\widebat{AE}+\widebat{DC}}{2}=\frac{\widebat{BC}}{2}\)
Góc \(\widehat{MBC}\) là góc tạo bởi tiếp tuyến và dây cung nên \(\widehat{MBC}=\frac{\widebat{BC}}{2}\)
Suy ra \(\widehat{MIC}=\widehat{MBC}\)
Xét tứ giác BMCI có \(\widehat{MIC}=\widehat{MBC}\) nên BMCI là tứ giác nội tiếp.
b) Ta có \(\widehat{MIC}=\widehat{MBC}\Rightarrow\Delta FIC\sim\Delta FBM\left(g-g\right)\)
\(\Rightarrow\frac{FI}{FB}=\frac{FC}{FM}\Rightarrow FI.FM=FB.FC\)
Ta cũng có \(\widehat{DBF}=\widehat{CEF}\Rightarrow\Delta BFD\sim\Delta EFC\left(g-g\right)\)
\(\Rightarrow\frac{FB}{FE}=\frac{FD}{FC}\Rightarrow FE.FD=FB.FC\)
Vậy nên \(FI.FM=FE.FD\)
c) Do PQ là đường kính nên \(\widehat{PTQ}=90^o\)
Suy ra \(\Delta FIQ\sim\Delta FTM\left(c-g-c\right)\Rightarrow\widehat{FTM}=\widehat{FIQ}\)
Lại có BIMC nội tiếp, BOCM cũng nội tiếp nên 5 điểm B, O, I, C, M cùng thuộc đường trong đường kính OM.
Suy ra \(\widehat{FIQ}=90^o\)
Vậy thì P, T, M thẳng hàng.
d) Ta thấy \(S_{IBC}=\frac{1}{2}BC.d\left(I,BC\right)\)
Do BC không đổi nên SIBC lớn nhất khi d(I; BC) lớn nhất.
Điều này xảy ra khi I trùng O hay tam giác ABC vuông tại B.
Vậy diện tích tam giác IBC lớn nhất khi AC là đường kính đường tròn (O).

a: góc BAC=góc BCA
=>sđ cung BC=sđ cung BA
b: xy//DE
=>góc AED=góc yAE=góc ABC
c: góc AED=góc ABC
=>góc ABC+góc DEC=180 độ
=>BCDE nội tiếp
Chọn đáp án C.
nên theo mối liên hệ giữa cạnh và góc trong tam giác ta có