Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Tính khoảng cách giữa hai mặt phẳng (A’B’D’) và (BC’D)
A. 3 3
B. 3
C. 3 2
D. 2 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
2 tháng 1 2017
Đúng(0)
Những câu hỏi liên quan
CM
6 tháng 8 2017
Đáp án D
Ta chứng minh (AB’D’)//(BC’D)
Khi đó d((AB’D’), (BC’D))=d(C,(BC’D))
Ta chứng minh (BC’D)⊥(ACC’). Rồi từ C kẻ CH ⊥ OC’suy ra CH ⊥(BC’D)
Ta có 
CM
11 tháng 7 2018
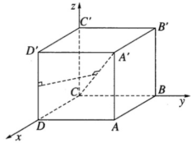
Ta chọn hệ trục tọa độ sao cho: C là gốc tọa độ, CD → = a i → ; CB → = a j → ; CC ' → = a k →
Trong hệ tọa độ vừa chọn ta có: C(0; 0; 0), A’(a; a ; a), D(a; 0; 0), D’(a; 0; a)
CA ' → = (a; a; a), DD ' → = (0; 0; a)
Gọi ( α ) là mặt phẳng chứa CA ' → và song song với DD ' → . Mặt phẳng ( α ) có vecto pháp tuyến là: n → = CA ' → ∧ DD ' → = ( a 2 ; − a 2 ; 0) hay x – y = 0
Phương trình tổng quát của ( α ) là x – y = 0.
Ta có:
d(CA′, DD′) = d(D,(
α
)) = 
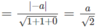
Vậy khoảng cách giữa hai đường thẳng CA’ và DD’ là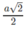 
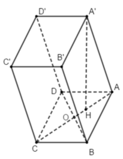
CM
1 tháng 1 2018
+ Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD
Ta có: A’B = A’D (đường chéo các hình thoi) ⇒ Tam giác A’BD cân tại A’ có O là trung điểm của BD ⇒ A’O ⊥ BD.
+ Hạ A’H ⊥ AC, H ∈ AC
Ta có B D ⊥ A C B D ⊥ A ' O ⇒ B D ⊥ A O A ' ⇒ A’H ⊥ BD
Do đó: A’H ⊥ (ABCD)
Vì (ABCD) // (A’B’C’D’) nên A’H chính là khoảng cách giữa hai mặt đáy.
+ Tính A’H
Ta có: AC = A D 2 + C D 2 − 2. A D . C D . cos 120 ° = a 3 ⇒ AO = a 3 2
Theo giả thiết ⇒ hình chóp A’.ABD là hình chóp đều, nên ta có:
AH = 2/3 AO = a 3 3
A’H = A ' A 2 − A H 2 = a 2 − a 2 3 = a 6 3
Vậy khoảng cách giữa hai đáy (ABCD) và (A’B’C’D’) là a 6 3 .
Đáp án B
CM
30 tháng 8 2017
Đáp án B
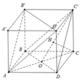
Ta có: C O = A B 2 2 = 2 . Dựng C H ⊥ C ' O (hình vẽ).
Do A B ' / / C ' D ; A D ' / / B D ⇒ A B ' D ' / / B C ' D
Khi đó d A B ' D ' ; B C ' D = d A ; C ' B D = d C ; B D C ' = C H = C O . C C ' C O 2 + C C ' 2 = 2 3 .
