Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

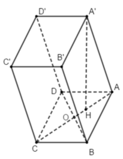
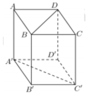
+ Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD
Ta có: A’B = A’D (đường chéo các hình thoi) ⇒ Tam giác A’BD cân tại A’ có O là trung điểm của BD ⇒ A’O ⊥ BD.
+ Hạ A’H ⊥ AC, H ∈ AC
Ta có B D ⊥ A C B D ⊥ A ' O ⇒ B D ⊥ A O A ' ⇒ A’H ⊥ BD
Do đó: A’H ⊥ (ABCD)
Vì (ABCD) // (A’B’C’D’) nên A’H chính là khoảng cách giữa hai mặt đáy.
+ Tính A’H
Ta có: AC = A D 2 + C D 2 − 2. A D . C D . cos 120 ° = a 3 ⇒ AO = a 3 2
Theo giả thiết ⇒ hình chóp A’.ABD là hình chóp đều, nên ta có:
AH = 2/3 AO = a 3 3
A’H = A ' A 2 − A H 2 = a 2 − a 2 3 = a 6 3
Vậy khoảng cách giữa hai đáy (ABCD) và (A’B’C’D’) là a 6 3 .
Đáp án B

a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: (SC;(ABCD))=(CS;CA)=góc SCA
Xét ΔBAC có BA=BC vàgóc BAC=60 độ
nên ΔBAC đều
=>AC=a
=>\(SC=\sqrt{SA^2+AC^2}=\dfrac{\sqrt{10}}{3}\cdot a\)
tan SCA=SA/AC=1/3
=>góc SCA=18 độ
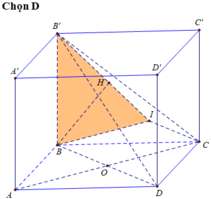



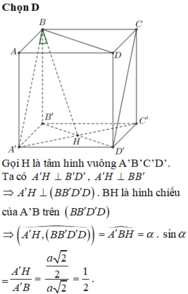
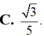
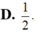

Đáp án D
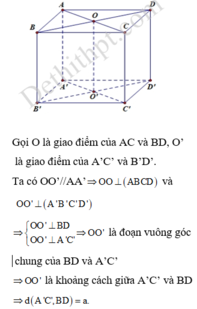
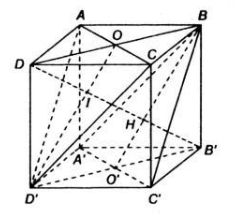
Ta chứng minh (AB’D’)//(BC’D)
Khi đó d((AB’D’), (BC’D))=d(C,(BC’D))
Ta chứng minh (BC’D)⊥(ACC’). Rồi từ C kẻ CH ⊥ OC’suy ra CH ⊥(BC’D)
Ta có